How Many Trailing Zeros Are Present in 1000 Factorial?
Written on
Chapter 1: Understanding Factorials
The factorial of a non-negative integer, denoted as n!, represents the multiplication of all positive integers up to n.
For instance, the factorial of 3 can be computed as 3! = 6.
Now, how do we determine the quantity of trailing zeros in 1000!? The essence of this challenge lies in identifying how often the number 5 appears in the prime factorization of 1000!.
To provide a clearer perspective, we can estimate that there are significantly more occurrences of 2 than 5 in the prime factorization of 1000!. Thus, our focus will be on counting the number of times 5 appears.
The first step is to identify all multiples of 5 up to 1000, as each of these contributes at least one factor of 5:
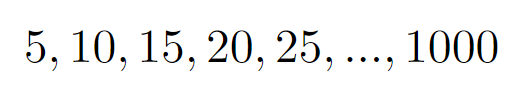
Calculating this gives us:
1000 / 5 = 200
This indicates there are 200 factors of 5.
Next, we consider the multiples of 25, as each of these has two factors of 5. However, we have already counted one factor of 5 from each in the previous step, so we only need to add one extra factor from each of these numbers:
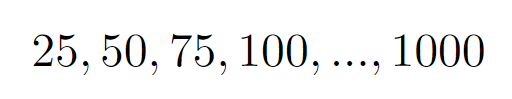
The calculation for this step is:
1000 / 25 = 40
Thus, we have an additional 40 factors of 5.
Now, we will evaluate the multiples of 125, as these numbers contain at least three factors of 5, two of which were already counted:
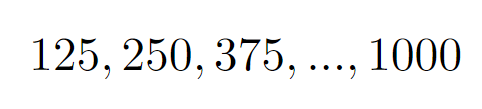
For this, we calculate:
1000 / 125 = 8
This yields 8 more factors of 5.
Finally, we note that one number, specifically 625, has four factors of 5:

Totaling these up gives us the complete number of trailing zeros:
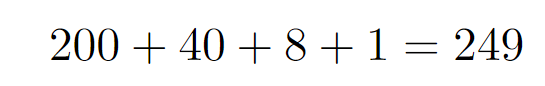
In conclusion, we can verify that there are indeed more 2s than 5s, as evidenced by 1000 / 2 = 500. Hence, we have successfully determined the number of trailing zeros in 1000!.
Isn’t it fascinating? What was your reasoning during this process? Feel free to share in the comments; I’d love to hear your thoughts!
Math Puzzles
Explore an assortment of intriguing math puzzles on Medium, covering topics from Algebra to Number Theory. Don’t forget to share these with your friends!
Chapter 2: Visual Insights
This video titled "Number system|1000! ends with how many zeros | find zeros" provides a visual explanation of the concept, making it easier to grasp the calculations involved.
The second video, "Counting the Zeros in 100 (and 1000) Factorial," further elaborates on the method for counting trailing zeros, enhancing your understanding of factorials.
Thank you for taking the time to read this! If you found this information valuable, a clap would be greatly appreciated. Your support motivates me to continue sharing insights.
