# Understanding the Count of Digits in a Number
Written on
Chapter 1: The Basics of Digit Count
Determining the number of digits in a number can be quite intriguing. To establish how many digits a particular number contains, we can use some mathematical techniques. The number of digits in a number is determined by the smallest power of 10 that is greater than that number. For instance, since 553298 is less than 1000000, which is (10^6), we can conclude that 553298 consists of 6 digits.
In this scenario, reading the number straightforwardly suffices. However, when dealing with powers of 2, like (2^{n}), the process becomes slightly more complex.
To approach this, we need to identify a power of 2 that is near a power of 10. For example, (2^3 = 8) is close to 10, but not close enough. Similarly, (2^7 = 128) is too far from 100. However, (2^{10} = 1024) is ideal for our purposes since it is approximately (10^3).
As we explore the relationship between these powers, we can raise both sides to smaller powers while keeping them relatively close:
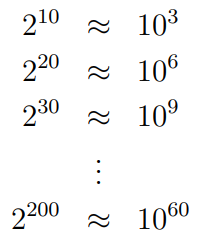
Chapter 2: Comparing Powers
The power (2^{10}) is slightly greater than (10^3). As we continue raising these powers, the left side (powers of (2^{10})) will eventually grow significantly larger than the right side (powers of (10^3)).
The key point to consider is whether the left side becomes ten times larger than the right side, as this indicates that the left side has one additional digit. Given that 1000 and 1024 are very close, this significant difference only occurs when the powers increase substantially. Therefore, we can reasonably equate the number of digits in (2^{n}) with (10^{n}).
Consequently, (2^{n}) has the same number of digits as (10^{n}), meaning it has 61 digits.
Challenge: It is anticipated that (2^{100}) has 301 digits. However, in reality, it has 302 digits due to the earlier mentioned relationship where the left side exceeded ten times the right side. Which power of (2^{n}) first becomes ten times greater than its corresponding power of (10^3)?
To solve this, you might want to use a calculator. Remember, (2^{10}) is approximately 1.024 times larger than (10^3). Utilizing logarithms could also assist in your calculations.
The first video, "Finding the Number of Digits in a Number," explores methods to determine how many digits are present in a given number using different mathematical techniques.
The second video, "How many digits are there in this number?", further elucidates the process of counting digits in numbers through engaging examples.