Exploring Algebra's Role in Ancient Greek Geometry Challenges
Written on
Chapter 1: A Journey Through Greek Geometry
Many of us have fond or frustrating memories of using a straightedge and compass during our school days. These simple tools connected us to the methods of ancient Greek geometry. While we used them, we were effectively engaging in geometry as the Greeks had done centuries ago.
When I was ten, my teacher presented our class with a challenge: could we construct a cube with double the volume of a unit cube using only a straightedge and compass? The restriction of not using a ruler meant we couldn’t make actual measurements. A few of us, particularly those with a passion for mathematics, spent considerable time attempting various methods, only to be met with disappointment when our teacher pointed out the flaws in our reasoning. After we exhausted this challenge, he posed another: could we create a square with the same area as a unit circle?
Looking back, it’s evident that our efforts were in vain. A decade later, as an undergraduate in Pure Mathematics, I would learn the rigorous proofs demonstrating the impossibility of doubling the cube or squaring the circle with just a straightedge and compass in a finite number of steps. What fascinated me about these proofs was their reliance on pure algebra, a field I had previously viewed as distinct from geometry. I couldn’t help but feel sympathy for the ancient Greeks, who pondered these questions without the tools needed to solve them.
Chapter 2: The Tools of the Trade
In this discussion, I aim to outline the fundamental steps that demonstrate the impossibility of doubling the cube and squaring the circle. While I will cover only the essential parts for brevity, I will also reference proofs for more complex results as necessary.
Section 2.1: Rings and Fields
In the mid-19th century, mathematician Richard Dedekind introduced a crucial concept in algebra: the ring. A ring is defined as a set R equipped with two binary operations, addition (+) and multiplication (×), satisfying specific criteria:
- R is a commutative group under addition, meaning:
- Addition is associative: (a + b) + c = a + (b + c) for any a, b, c in R.
- Addition is commutative: a + b = b + a for any a, b in R.
- There exists an additive identity, 0, where a + 0 = a for any a in R.
- Every element a in R has an additive inverse, denoted -a, such that a + (-a) = 0.
- R is associative under multiplication, and there exists a multiplicative identity, 1.
- Multiplication distributes over addition: a × (b + c) = (a × b) + (a × c) and (a + b) × c = (a × c) + (b × c) for any a, b, c in R.
While multiplication in a ring does not have to be commutative, many familiar rings, like the integers, exhibit this property and are classified as commutative rings.
Section 2.2: Properties of Fields
To enhance the structure of a ring, we can define a field, which is a commutative ring with certain additional properties. A field F has:
- A multiplicative identity (1) distinct from the additive identity (0).
- A multiplicative inverse for every element in F, except for 0.
For example, the set of rational numbers forms a field, as does the set of real numbers. It’s noteworthy that fields can be finite, such as the Galois Field GF[2], which comprises just two elements: 0 and 1.
The first video, "Classical problems of Greek geometry," delves into the challenges posed by ancient geometric constructions and their algebraic implications.
The second video, "Greek geometry (a) | Math History | NJ Wildberger," explores the historical context of these geometric problems and their significance in mathematics.
Chapter 3: The Intersection of Algebra and Geometry
Section 3.1: Constructibility and Limitations
We must acknowledge the constraints of compass and straightedge constructions. These rules define valid constructions:
- Any straight line passing through two points is valid.
- Any circle centered at one point intersecting another point is valid.
- Any intersection points from valid constructions are also valid.
Using these rules, we can define a number q as constructible if we can create a line of length q starting from a unit line in a finite number of steps using a compass and straightedge.
Fact 3.2: The set of all constructible numbers forms a field under standard addition and multiplication, meaning that all rational numbers are indeed constructible.
We can now leverage our understanding of fields. Any straight line or circle formed through points with coordinates in R corresponds to polynomials of degree 1 and 2, respectively. This leads us to prove two essential facts:
- The intersection points of any two lines with coefficients in R are also in R.
- The intersection points of a line and a circle, or two circles with coefficients in R, lie in a field extension of degree at most 2 over R.
Fact 3.3 establishes that any constructible number must reside in a field of degree 2^k over R for some positive integer k, indicating that all constructible numbers are algebraic over R.
Section 3.2: The Impossibility of Doubling the Cube and Squaring the Circle
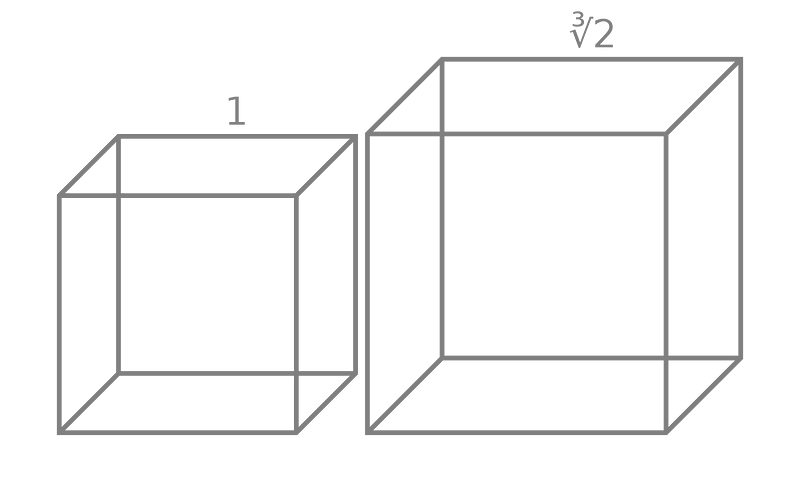
Fact 3.4: Doubling the unit cube is impossible using finite steps with a compass and straightedge. To accomplish this, we need to establish that √2 is constructible. However, since √2 lies in a field extension of degree 3 over R, it cannot be constructible.
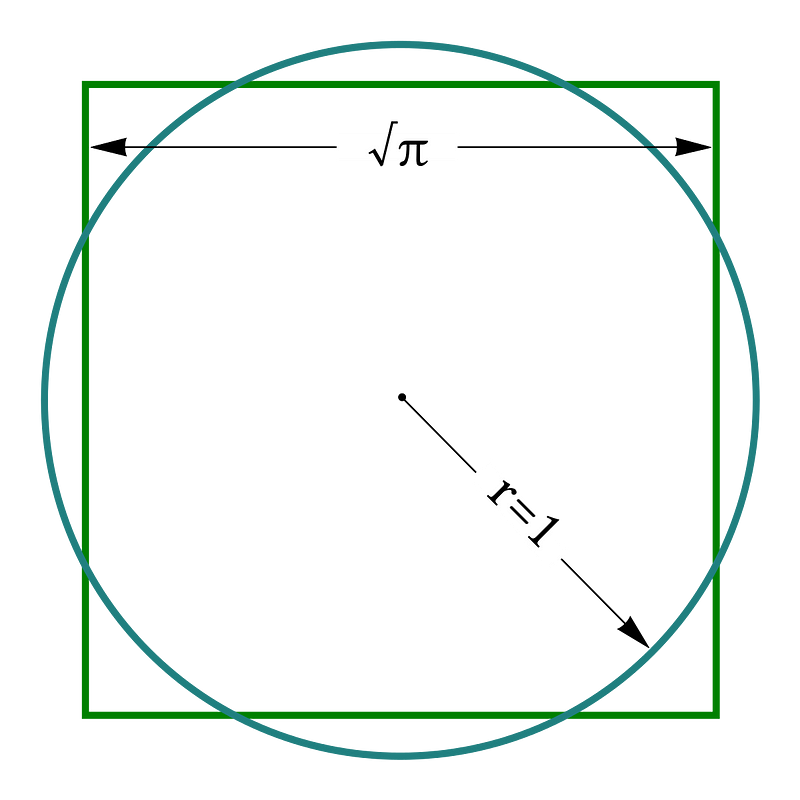
Fact 3.5: Squaring a circle with a unit radius is also impossible. To square the circle, we must prove that π is constructible. Lindemann established in 1882 that π is transcendental over R, indicating that it lies in an infinite degree field extension over R, and consequently, π cannot be constructible.
The connection between abstract algebra and ancient Greek geometry is both captivating and inspiring. I encourage you to explore these concepts further. For instance, while it is established that any angle can be bisected, try proving the impossibility of trisecting a 60-degree angle.
What are your thoughts on the interplay between algebra and classical geometry? Feel free to share your insights.