Innovative Methods for Measuring Elevator Travel Distance
Written on
Chapter 1: Introduction to Elevator Physics
In the realm of physics, intriguing questions often arise. Consider this scenario: you have a block of aluminum placed on a digital scale, which reads 102 grams. This scale is positioned on the floor of an elevator. When someone presses a button for a floor, the elevator begins to move, causing a change in the scale’s reading (for more information on how a scale operates, refer to my previous article).
This experiment raises two key inquiries: Did the elevator ascend or descend? And what distance did it cover?
To address the first question, we notice that the scale initially shows 102 grams. As the elevator starts moving, the reading increases to approximately 109 grams and then stabilizes back at 102 grams. The increase indicates that the elevator is accelerating upwards, confirming it is indeed moving to a higher floor.
Now, determining the distance traveled is more complex. Let's begin with a rough estimation before delving into a more detailed calculation.
Section 1.1: Rough Estimation of Distance
Observing the video alone may not yield precise values for acceleration, but we can derive an approximate starting point. The following force diagram illustrates the aluminum block while the elevator accelerates upwards.
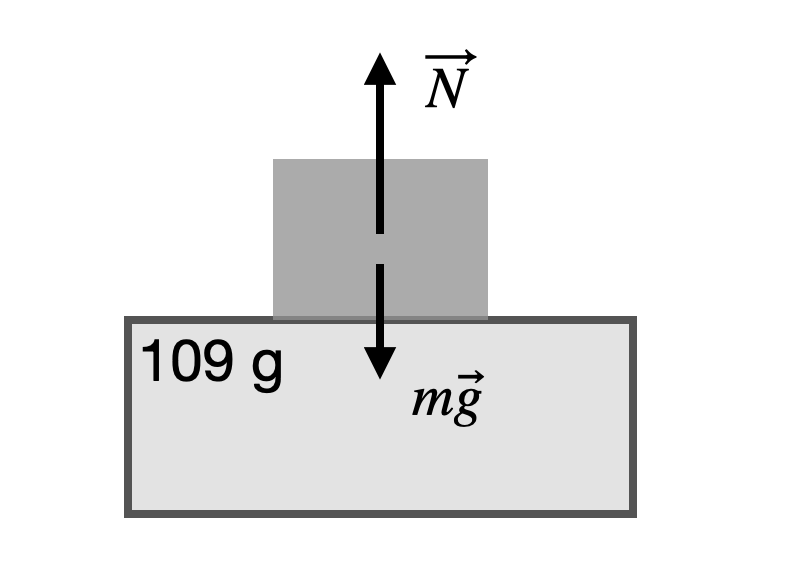
According to Newton’s second law, we can formulate an equation for the forces acting on the block.
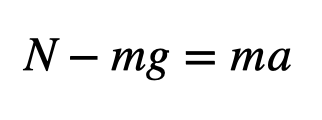
The normal force corresponds to the scale reading. Assuming this yields a reading of m2, we can derive the acceleration:
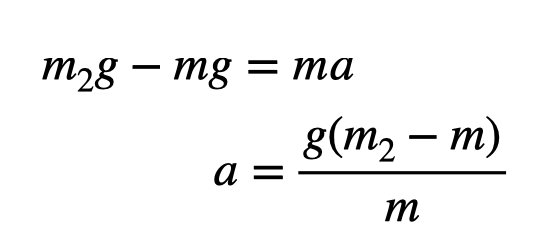
With readings of 109 grams and 102 grams, we calculate an acceleration of approximately 0.672 meters per second squared. This seems reasonable. Here's the plan to move forward:
- Assume the elevator accelerates consistently for a short time.
- Use this time and acceleration to find the velocity during most of the journey (ignoring the brief acceleration phase for now).
- Utilize the travel velocity and the time taken to calculate the distance.
While this is a rough estimation, it will help us determine whether the elevator traveled 2 meters or 20 meters.
Looking at the video, we note that the acceleration lasts for 1.5 seconds (denoted as ?t1) and the upward movement lasts about 5 seconds (?t2). Using the definition of acceleration, we can calculate the travel velocity (v_2).
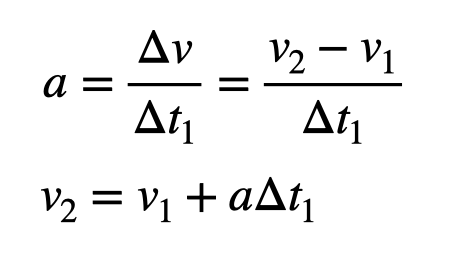
Starting from rest (v_1 = 0), we estimate that the elevator reaches a speed of roughly 1.0 meter per second. For the constant velocity phase, we can apply the formula for constant velocity.
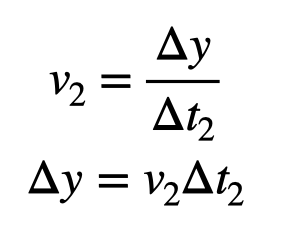
Using the travel velocity and time, we estimate the elevator ascended approximately 5 meters. Admittedly, I overlooked the distance covered during both acceleration phases, but we can check the actual height using a laser range finder, which measures the distance between floors at 3.9 meters.
Section 1.2: Enhanced Measurement Techniques
While the scale provides a helpful visual, its resolution and response time might limit accuracy. Thankfully, modern smartphones come equipped with accelerometers, allowing for more precise measurements. Using an app like PhyPhox, I can gather acceleration data by placing my phone on the elevator floor.
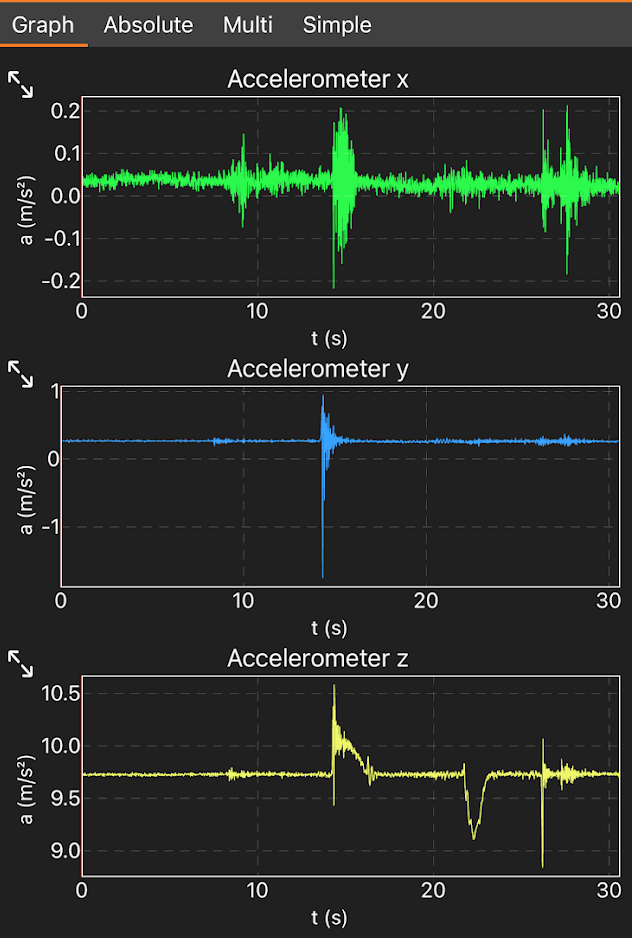
The data reveals significant upward acceleration, while noise from the elevator's movement is minimal. After filtering out the initial and final stationary periods, we obtain a comprehensive acceleration plot.
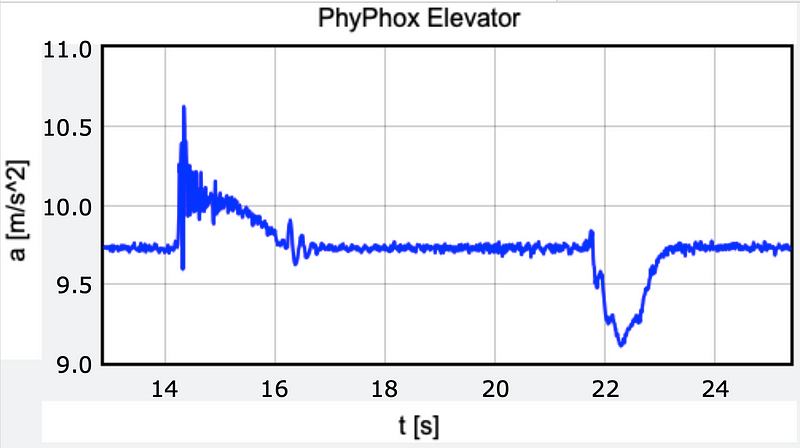
This data collection allows for a more detailed analysis, capturing acceleration at 100 samples per second. Before and after the doors close, we observe an acceleration of 9.73 m/s². This discrepancy from the expected 9.8 m/s² aligns with Einstein's Equivalence Principle, which suggests no difference exists between gravitational force and acceleration.
After approximately 14 seconds, a positive acceleration indicates the elevator's upward motion, followed by a return to 9.73 m/s², signifying constant velocity. Around 22 seconds, negative acceleration shows the elevator slowing down.
To quantify this data, we use the acceleration readings to derive vertical velocity over time. Given the short intervals between readings, we can assume consistent acceleration within each segment.
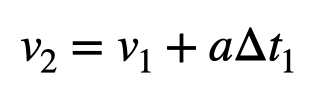
This method is akin to numerical integration, leading to a clearer understanding of the elevator's behavior. Ultimately, we can apply the velocity data to find the elevator's position over time.
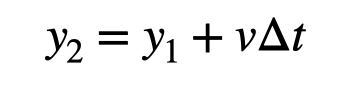
The final position calculation yields approximately 3.5 meters, slightly below the earlier measurement of 3.9 meters. While discrepancies exist, this approach offers a more engaging exploration than merely riding an elevator.
The second video provides additional insights on calculating the normal force and apparent weight, further enriching our understanding of elevator physics.