A Challenging Trigonometry Problem You Can Attempt
Written on
Chapter 1: Introduction to the Problem
Can you tackle this intriguing trigonometry question? It originally appeared in a Cambridge University mathematics entrance examination back in 1987. The beauty of this problem lies in its simplicity and complexity, as it only requires fundamental high school trigonometry to solve. The problem is presented as follows:
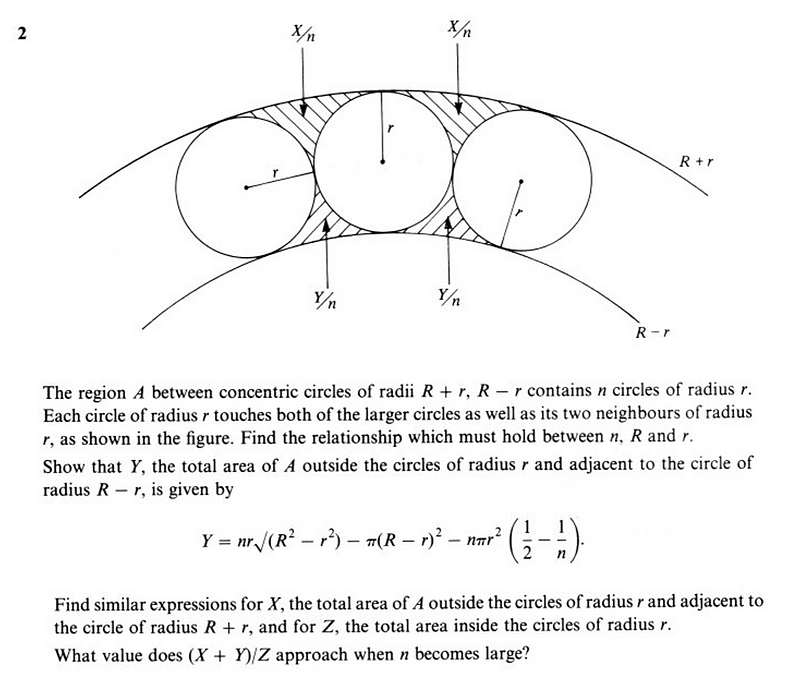
Before I share my solution, I encourage you to attempt it on your own and see how far you can get.
Section 1.1: Solution to Part One
To begin, we can observe that by connecting the centers of the small circles, we form a regular polygon with n sides, each measuring 2r. Focusing on one of these sides, if we connect both ends to the center of the smaller circle with radius R-r, we create an isosceles triangle. This triangle has two equal sides of length R and a base of length 2r, with an angle at the center measuring 360/n degrees, which can also be expressed in radians as 2π/n. By dividing this triangle along its line of symmetry, we create a right triangle where one side measures r, the opposite angle is π/n, and the hypotenuse is R. This leads us to the conclusion that r/R = sin(π/n), or equivalently, r = Rsin(π/n).
Subsection 1.1.1: Visualizing the Problem
Section 1.2: Solution to Part Two
Next, we need to find the area Y, which represents the shaded region between the n small circles and the larger inner circle. We will take a systematic three-step approach to compute this area:
- First, we will determine the area of the polygon mentioned earlier.
- Next, we will subtract the area of the inner circle with radius R-r.
- Finally, we will subtract the areas of the n segments of the small circles that lie within the polygon.
It's important to note that the area Y is composed of three parts, where the latter two are subtracted from the first, suggesting our method should lead us to the correct answer.
For part A, we can find the area of the polygon by dividing it into n isosceles triangles, each with a base of 2r and equal sides of R. Using the Pythagorean theorem to find the height, we have √(R²-r²). Hence, the area of one triangle is 0.5 * 2r * √(R²-r²) = r√(R²-r²). Consequently, the total area of the polygon is nr√(R²-r²), which corresponds to the first term in the expected result.
For part B, the area of the inner circle is simply π(R-r)², aligning with the second term of the expected result.
For part C, we need to calculate the area of the segment of each small circle that resides within the polygon. The inner angle of the regular n-gon is π((n-2)/n), which means the area of this segment for each small circle is πr²(1/2 - 1/n). When multiplied by n, this provides us with the final term of our expected result.
Section 1.3: Solution to Part Three
To find X, the area of the outer shaded segment, we will adopt a similar logical strategy:
- Begin with the area of the entire outer circle with radius R+r.
- Subtract the area of the polygon.
- Subtract the areas of the segments of the small circles that extend beyond the polygon.
For part A, the area is π(R+r)². For part B, as previously calculated, it is nr√(R²-r²). For part C, since the segments outside the polygon represent (1/2)+(1/n) of each circle, we find their total area as πr²((1/2)+(1/n)).
Thus, the area of X can be expressed as π(R+r)² - nr√(R²-r²) - πr²((1/2)+(1/n)).
Section 1.4: Conclusion and Final Thoughts
For the last part, we know Z = nπr², which corresponds to the combined area of n circles each with radius r. When we add X and Y, some terms will cancel out, resulting in:
X + Y = π(R+r)² - π(R-r)² - nπr²
By simplifying and dividing this expression by Z, we arrive at the final simplified result:
(X+Y)/Z = (4R/nr) - 1
Recalling that r = Rsin(π/n), we can substitute this back in to yield:
(X+Y)/Z = (4/n sin(π/n)) - 1
What does this imply as n approaches infinity? As n increases, π/n becomes very small, and we find that sin(x) ≈ x for small values of x. Thus, for very large n, we conclude that:
(X+Y)/Z ≈ (4/π) - 1
This is a fascinating result that is challenging to verify through computation, as the precision of π significantly affects the accuracy of calculations when n becomes very large.
I hope you found this problem as engaging as I did. Feel free to share your thoughts in the comments below.
Chapter 2: Additional Resources
The first video titled "Difficult Trigonometry Questions: ACT MATH" delves into similar challenging problems, providing explanations and strategies to enhance your understanding.
Another insightful video, "Solving More Difficult Trig Equations," offers a deeper look into complex trigonometric equations and their solutions.