Chapter 1: Defining Irrational Numbers

Irrational numbers are defined as real numbers that cannot be expressed as fractions or ratios of integers. Rational numbers include examples like 1/2, 3/5, and 7/4. While all types of numbers, including irrationals, can be expressed in decimal form, the decimal representation of irrational numbers is unique; it neither terminates nor forms a repeating sequence, unlike recurring decimals such as 1/3 = 0.333... Among these irrational numbers is π, which represents the ratio of a circle's circumference to its diameter.

Figure 1 illustrates the set of real numbers R, which encompasses rational numbers Q, integers Z within Q, natural numbers N within Z, and irrationals RQ. Notably, the set of irrational numbers lacks a unique symbol, unlike the other sets.

Numerous ancient civilizations have approximated the value of π (see this link). However, it wasn't until the 17th century, following the advent of calculus by Isaac Newton and Gottfried Leibniz, that more accurate estimations through infinite series emerged. One notable series was identified by the Indian mathematician Madhava of Sangamagrama. For x=1, this series transforms into the well-known Leibniz formula for π:

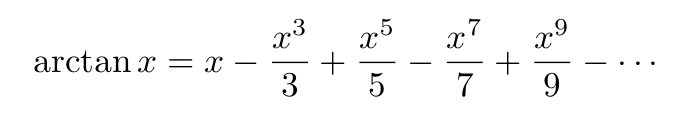
This formula, while historically significant, converges rather slowly.

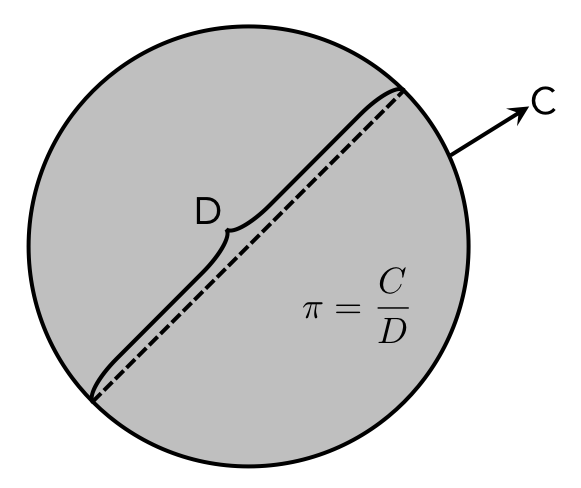
Figure 2 exemplifies π, which serves as a classic case of an irrational number.

Another widely recognized irrational number is the square root of 2, discovered by followers of the esteemed philosopher Pythagoras of Samos. Legend has it that they initially concealed this finding and purportedly executed Hippasus of Metapontum for disclosing it.

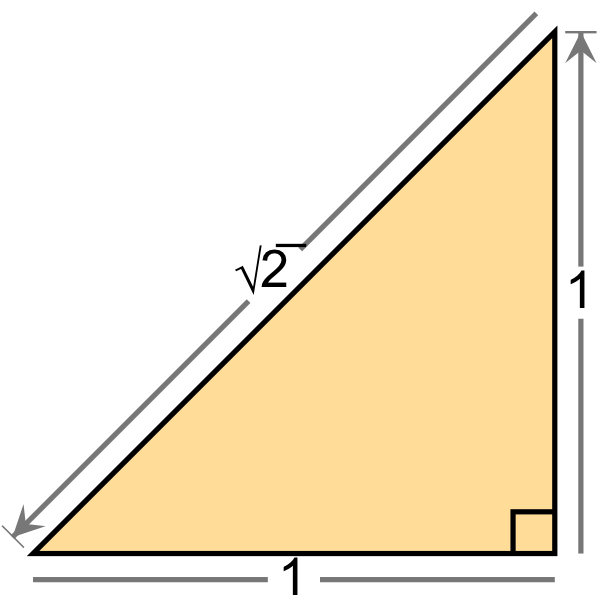
Figure 3 illustrates the square root of 2, underscoring its classification as an irrational number.

Chapter 2: A Simple Proof of π's Irrationality

In this section, we will present a straightforward proof of the irrationality of π, drawing inspiration from mathematician Ivan M. Niven. To initiate, we will assume the opposite of our intended conclusion: that π² is rational:

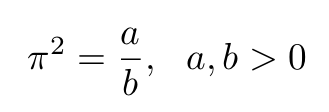
Equation 6 posits that π² is rational, which contradicts our goal.

To proceed, we construct the following function:

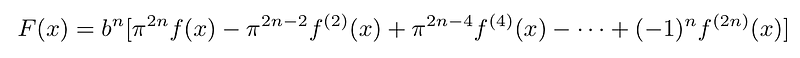
The second derivative of this function, which will be relevant later, is given by:

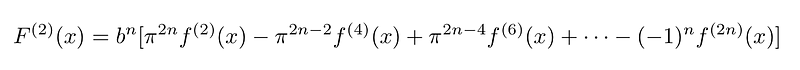
Figure 4 depicts the mathematician Ivan M. Niven, who contributed to the proof of π's irrationality.

As established, both f(x) and all its derivatives yield integer values at x=0 and x=1. This leads us to conclude that F(0) and F(1), and consequently F(1) + F(0), are integers as well. We can apply the following identity:

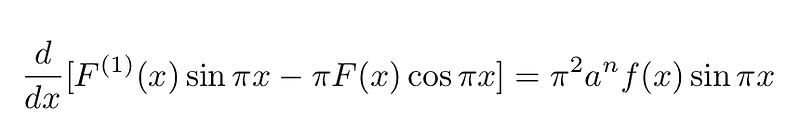
By integrating both sides, we arrive at:

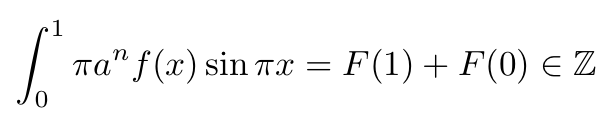
Using our earlier findings, we derive:

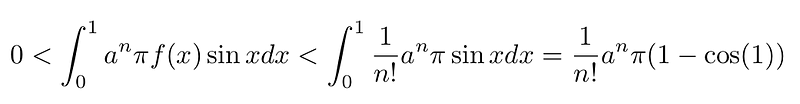
For sufficiently large n, we find:

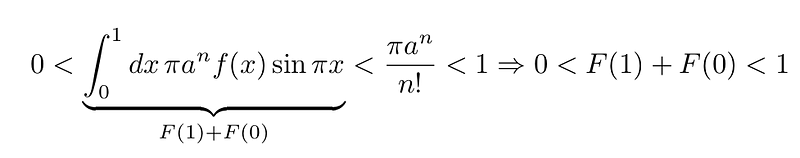
This outcome contradicts our earlier assertion that F(1) + F(0) is an integer. Therefore, our initial assumption (Equation 6) must be incorrect, and π² is irrational. Consequently, if π were rational, π² would also be rational. Hence, we conclude that π is irrational, completing the proof.

The elegance and simplicity of this argument highlight the intrinsic beauty of pure mathematics. For more interesting materials on mathematics, physics, data science, and finance, feel free to explore my personal website at www.marcotavora.me.

The first video, titled "How to prove a number is irrational - Specialist Math Australia," offers insights into the concept of irrational numbers, enhancing our understanding of this mathematical phenomenon.

The second video, "Proof: √3 + √2 is irrational," provides additional context and examples related to irrational numbers, further illustrating their properties and significance.