# Understanding Einstein's Theory of Relativity: A Comprehensive Guide
Written on
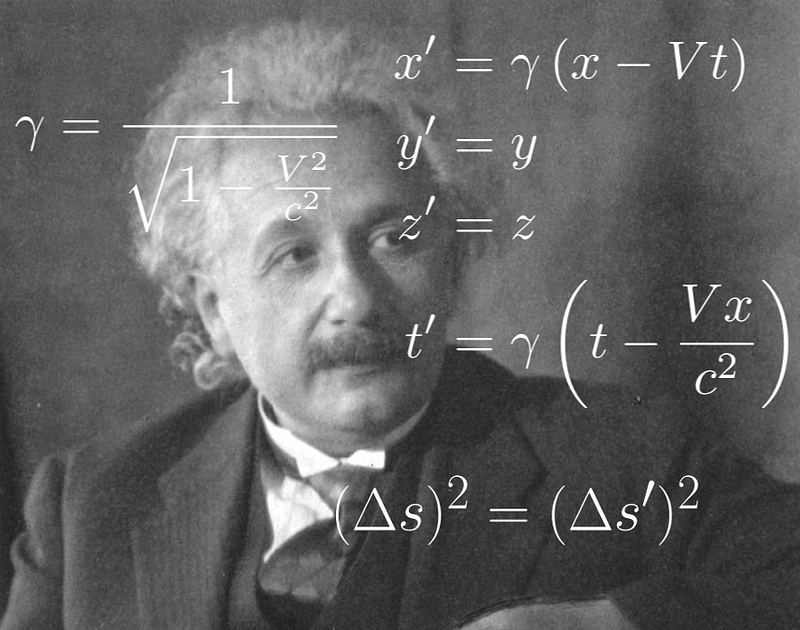
Einstein's Theory of Relativity is often regarded as one of the most significant breakthroughs in scientific history, rivaling only Newton's laws of mechanics in its impact on physics. Despite its importance, many people find special relativity challenging to grasp, and a plethora of misinformation abounds online and in the media. This confusion is exacerbated by its reputation for complexity, which is largely unwarranted.
The core principles of relativity are not overly complicated. This article aims to clarify these foundational concepts by tracing the evolution of physics from Galileo to the present, illustrating the need for adjustments to the 19th-century laws of physics, detailing how special relativity emerged from these changes, and examining its consequences.
Reference Frames, Covariance, and Galilean Relativity
The essence of relativity is that observers moving relative to one another must concur on the laws of physics. When two observers are in relative motion, they occupy different reference frames. If their relative velocity remains constant, these frames are termed inertial. A theory is considered covariant if all observers in inertial frames agree on it. Our focus will be solely on inertial frames.
Imagine an observer at rest in frame S at the origin of a coordinate system (x,y,z), while another observer at rest in frame S' is at the origin of a different coordinate system (x',y',z'). If the observer in S observes the origin of S' moving to the right at a constant velocity V, we describe this configuration as standard configuration:
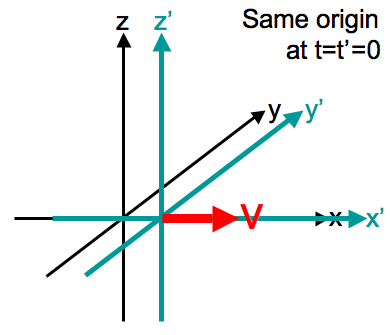
We will assume that S and S' are always in this standard configuration.
If an event occurs at point P at time T' in frame S and another at point Q at time T, with L representing the distance between P and Q and ?T = T' - T, we can analyze how these events are perceived in the other reference frame. Before Einstein's contributions, the following assumptions were standard:
- Distance is absolute: L = L'
- Time is absolute: ?T = ?T'
Lengths were determined using the Pythagorean theorem: L² = (?x)² + (?y)² + (?z)², where ?x, ?y, and ?z denote displacements along the respective axes. Quantities that remain numerically constant across all inertial frames are termed invariant.
Let x, y, z, and t be the coordinates tied to frame S, while x', y', z', and t' pertain to frame S'. The assumptions about distances and time intervals imply a relationship between these coordinate systems:
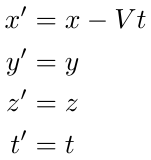
This is known as the Galilean transform. Galilean relativity posits that the laws of physics are covariant under this transformation. We can verify this for Newtonian physics. If Newton's laws hold true in frame S':
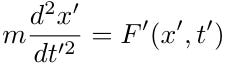
Here, F'(x',t') represents an arbitrary force measured in frame S', while F(x,t) denotes the same force in frame S. If the observer in S' determines F'(x',t') by checking specific values for x' and t', the observer in S should get the same results since both reference frames experience no relative acceleration:
By substituting x' = x - Vt and t' = t into the derivative, we obtain:
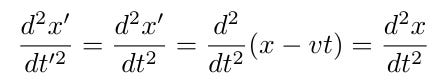
Consequently, we find that:
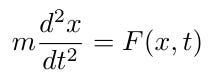
Thus, Newtonian physics remains covariant under the Galilean transform. However, does this hold true for all physical laws?
Examine Maxwell's equations in a charge- and current-free space:
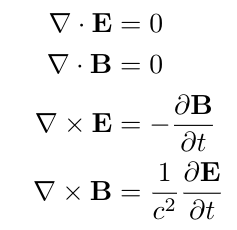
Taking the curl of the third equation yields the wave equation for the electric field vector E:
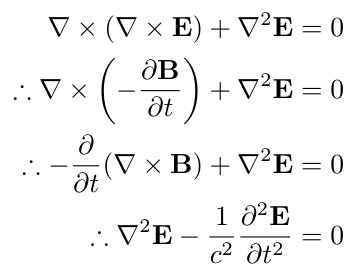
This equation indicates that disturbances in the electric field propagate at a constant speed c, the speed of light. If we consider an electric field whose sole component lies in the x-direction and is independent of y or z, we investigate how this wave equation transforms in frame S':
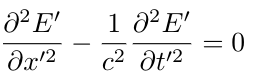
This must transform into:
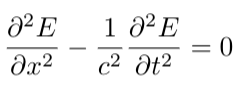
Next, we analyze the derivatives under the chain rule:
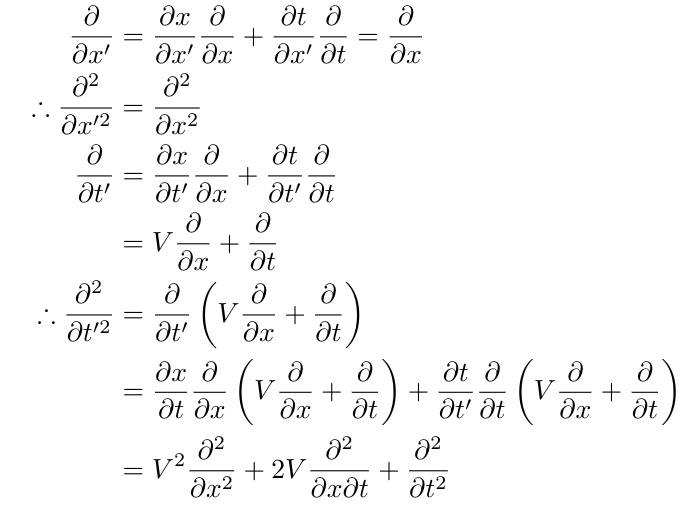
This leads to the following transformation of the wave equation as observed from frame S':
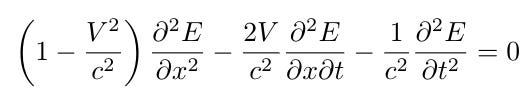
Here lies a conflict: observers in varying inertial frames will disagree on the laws governing light propagation. To resolve this, we must accept at least one of the following statements:
- Maxwell's equations are incorrect.
- There exists a single special reference frame where Maxwell's equations hold true, specifically the rest frame of the luminiferous ether.
- The Galilean transform is flawed, leading to erroneous assumptions about space and time.
The first statement can be dismissed outright; Maxwell's equations are well-established empirical truths. The second statement can be rejected based on the numerous failed attempts to detect the ether in the late 19th century. This leaves us with the third assertion.
The Lorentz Transform and Einstein’s Theory of Relativity
In 1892, Hendrik Lorentz demonstrated that Maxwell's equations are covariant under the following transformation:
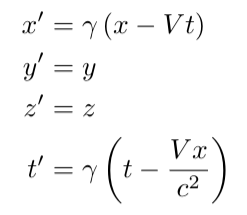
Here, ? is known as the Lorentz factor:
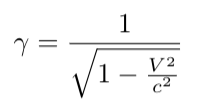
Newton's laws can also be adjusted to be covariant under this transformation, which will be explored in a follow-up article.
This transformation is termed the Lorentz transform. Unfortunately, Lorentz misinterpreted its physical significance, attributing it to Earth's motion relative to the luminiferous ether.
Einstein corrected this interpretation in his 1905 paper, On the Electrodynamics of Moving Bodies, laying the groundwork for what we now refer to as special relativity. He based his work on two key postulates:
- The laws of physics are identical across all inertial reference frames.
- The speed of light remains constant across all inertial reference frames, meaning it is invariant.
These principles allow us to derive the Lorentz transform, although they necessitate a shift in our understanding of space and time.
Time Dilation
Let S' represent the rest frame of a train, which is in standard configuration with S, the rest frame of an observer on the platform. An experiment is conducted on the train, during which a certain physical process unfolds over an interval ?t'. Observers on the platform will perceive this same event as occurring over a time interval ?t, where ?t and ?t' are related by:
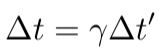
Since ? > 1, this phenomenon is termed time dilation. If, according to the train's observer, a laser pulse ascends from point A', reflects off a mirror at point B', and returns to a detector at point C', which is adjacent to A':
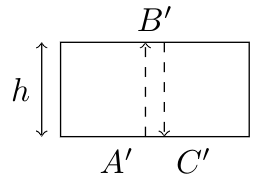
The total distance covered by the laser pulse amounts to 2h, traveling at speed c, thus:
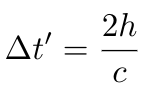
Next, let’s consider the perspective of the observer on the platform. As the laser pulse travels at a constant speed between the emitter and the mirror, the train simultaneously advances to the right. To the platform observer, the path traced by the laser pulse forms a triangle:
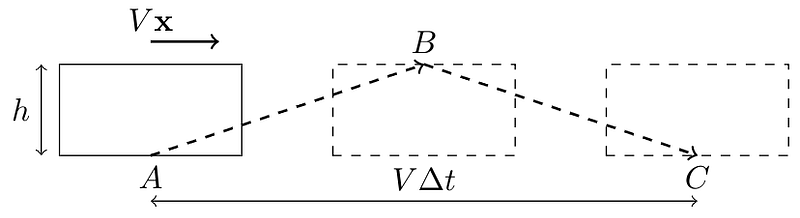
Utilizing the Pythagorean theorem, we can determine the length of line AB as:
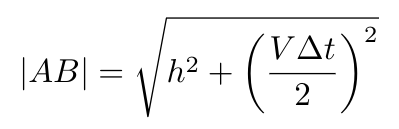
The total path length doubles, and since the speed of light remains constant in both reference frames, this distance must equal c?t, yielding:
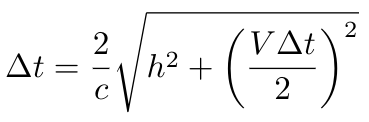
By substituting h = c?t'/2 into the equation for ?t and squaring both sides, we arrive at:
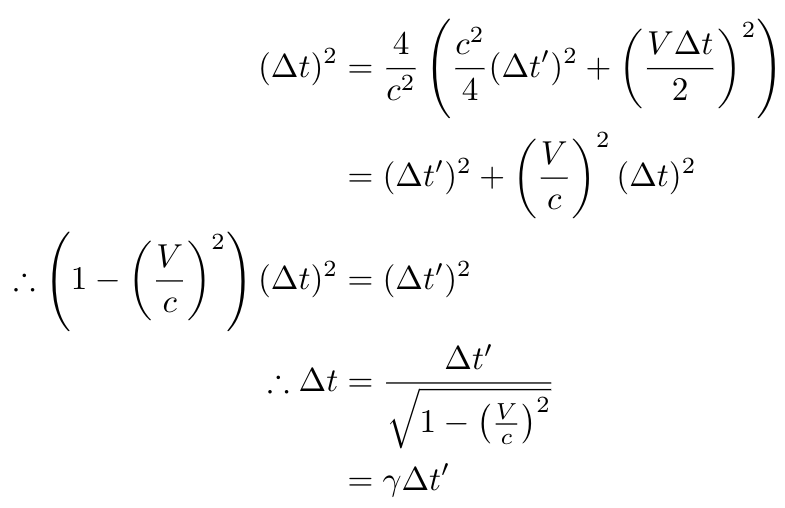
This illustrates that, due to the invariance of the speed of light, time experiences dilation across different reference frames. It accounts for the phenomenon where moving clocks appear to tick more slowly: if a clock on the train ticks every second, then to an observer on the ground, the intervals between ticks are dilated.
Demonstration: Muon Decay
A muon is a subatomic particle that resembles an electron, but is roughly 207 times heavier. The weak force, one of the four fundamental forces, causes a muon to decay into an electron and two other particles: an electron antineutrino and a muon neutrino:
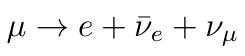
Muons have a half-life of approximately 2.2 microseconds. Thus, if a sample contains 100 muons, it will take around 2.2 microseconds for half of them to decay into electrons.
Muons form in the upper atmosphere when cosmic rays collide with gas molecules at an altitude of roughly 15 kilometers. At sea level, muon detectors typically register one muon per square centimeter per minute, with an average velocity of about 0.995c upon detection. Ignoring relativity, the time required for a muon to reach sea level would be calculated as 15,000m/0.995c ~ 50 microseconds, translating to about 23 half-lives. Given the muon flux at sea level is 1/s·cm², this implies the production rate at altitude would be 2²³/s·cm², an unrealistic figure.
Now, let’s consider the implications of special relativity. For particle decay, what matters is not how much time passes for the observer, but how much time elapses for the particles. If these particles are moving significantly faster than the observer, then because of time dilation, while a time interval ?t passes for the observer, a shorter interval ?t' = ?t/? elapses for the particles.
For V = 0.995c, ? ~ 10. Thus, while the observer perceives the muons taking about 50 microseconds to descend to sea level, for the muons, it only takes about 5 microseconds, or roughly 2.3 half-lives. Consequently, if the sea-level muon flux is 1/s·cm², the production rate at 15km altitude would be about 4.5/s·cm², a significantly more plausible number.
From the muons' perspective, they observe the ground approaching them at a speed of 0.995c. They perceive themselves reaching the ground (or the ground reaching them) in just 5 microseconds. But how can they cover 15,000 meters in 5 microseconds while traveling at a mere 0.995c? The answer is straightforward: they don't.
Length Contraction
An observer at rest in frame S sees a particle with velocity Vx pass a marker at point A at time t = 0. After a time ?t, she sees it pass another marker at point B, both positioned along the x-axis and separated by distance L. In the rest frame of the particle, denoted as S', the particle is stationary, and the two markers are moving towards it at velocity -Vx. The first marker passes the particle at time t' = 0, while the second passes it at time ?t' = ?t/?. Thus, we observe that L' = L/?, indicating that length contracts in the moving frame.
This explanation resolves the earlier question: the muons are not required to traverse the full 15,000-meter distance seen by an observer on the ground. Instead, in their rest frame, the distance is merely 1500 meters.
This phenomenon refers to the contraction of space as perceived by an observer in the rest frame of a moving object. There's also a reciprocal version of this principle: moving objects appear contracted. If S' denotes the rest frame of a rod perceived as moving at velocity Vx by an observer in frame S, the observer cannot distinguish whether she is moving relative to the rod or vice versa. If she were moving relative to the rod, she would see space contracted, leading the rod to appear shorter than its rest length. This is equivalent to stating that the rod appears shorter due to its motion, given that neither the observer nor the rod can ascertain their relative motion.
The Lorentz Transform
Now, we can demonstrate that the Lorentz transform links the coordinate systems of two reference frames in standard configuration. We will show that:
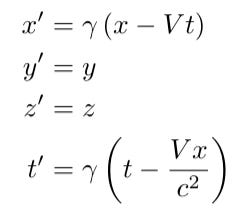
Given that the velocity of S' relative to S is constant and directed entirely along the x-axis, by symmetry, it follows that y' = y and z' = z.
To move forward, we introduce a new quantity termed the spacetime interval (?s)²:
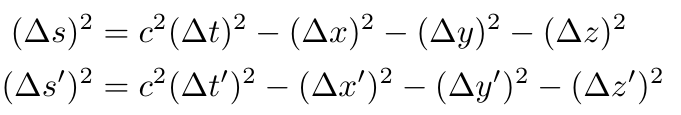
We will demonstrate that the spacetime interval is invariant, meaning that (?s)² = (?s')² across all pairs of reference frames S and S'.
Suppose an observer at rest in frame S emits a laser pulse that travels distance L in time ?t. In frame S', this pulse travels distance L' in time ?t'. The invariance of c implies that:
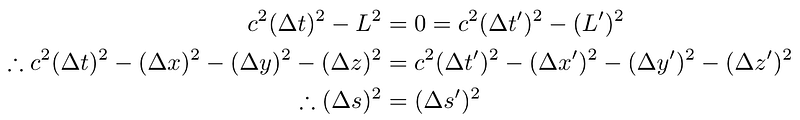
The remainder of the derivation for the Lorentz transform adheres to the approach Einstein utilized in his well-known book on relativity. By disregarding the delta symbols in the second line above and noting that y' = y and z' = z, these components cancel out of the equation. We can reframe the equation as:
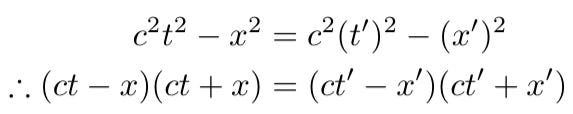
This allows us to express:
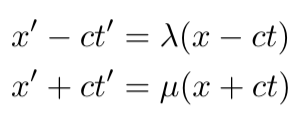
By adding the second equation to the first, we derive an expression for x', and by subtracting the first equation from the second, we obtain one for ct':
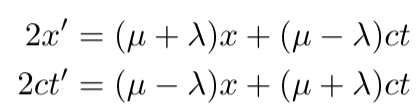
Next, we will make the following assignments:
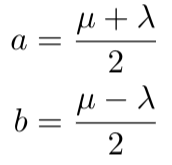
This results in a linear system for x' and ct':
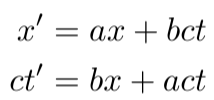
As the origin of the primed coordinate system moves with velocity Vx, we can set its position vector as (Vt,0,0), thus letting x' = 0 coincide with x = Vt. The first equation leads us to:
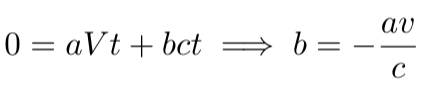
At this point, the system of equations simplifies to:
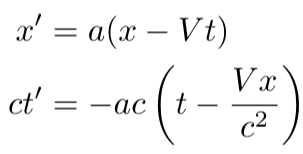
To solve for ?, substitute these into the expression for the invariance of the spacetime interval, c²(?t')² - (x')² = c²(?t)² - x²:
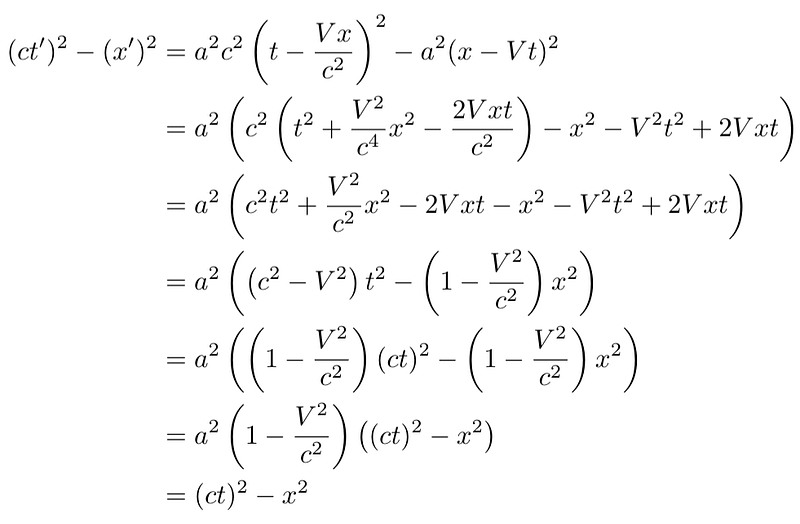
This implies:
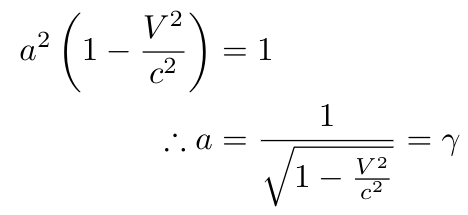
Substituting this result into the formulas we derived for x' and ct', we obtain the Lorentz transform:
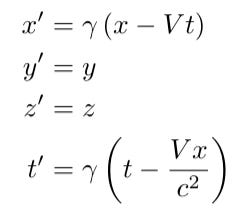
Thus, we have successfully derived the Lorentz transform from fundamental physical principles.
Demonstration: The Classical Limit
The Lorentz transform appears markedly different from the Galilean transform. How could physicists have held such misconceptions for so long?
Consider a fighter jet traveling just above the speed of sound, with V = 350 m/s. Thus, V²/c² ~ 1.4×10?¹². The most effective way to approximate ? for small values of V²/c² is by employing the binomial approximation:
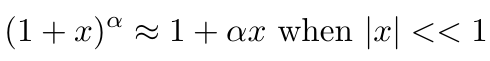
This yields an accurate estimation for ?:
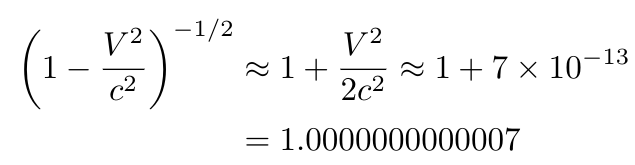
Consequently, for speeds nearing the speed of sound, non-relativistic physics remains precise to parts per trillion (12 decimal places). It’s worth noting that even this relatively "low" speed was practically unattainable for experimentalists prior to the 20th century and would never have been encountered in everyday life, clarifying why it took nearly 300 years since Galileo's time for any discrepancies to be recognized.
Spacetime
It is crucial to understand that time dilation and length contraction are inherent properties of space and time themselves. They are not artifacts of forces that cause clocks to tick more slowly depending on the observer, nor do relativistic speeds induce forces that stretch or compress objects. Neither are they products of measurement errors or optical illusions that lead observers in different frames to misjudge the lengths of objects or the rates at which clocks tick. When observers in differing frames report varying lengths for measuring rods or different ticking frequencies for clocks, they are all accurate, as lengths and time intervals are not invariant; this is simply how space and time function.
Classical physics operates within three-dimensional Euclidean space, E³, which comprises all ordered triples of real numbers (x,y,z) alongside sufficient topological structure to define concepts like "distance" and "point," accompanied by a function known as the Euclidean metric, which states that the distance between two points P? = (x?,y?,z?) and P? = (x?,y?,z?) is defined as:
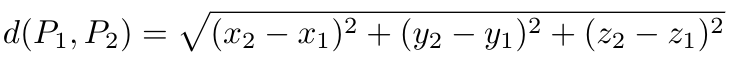
In classical physics, if an event occurs at point P? at time t? and another at P? at time t?, separated by distance L and time ?t = t? - t?, the best we can assert is that the two events occurred L meters apart, with the second event taking place ?t seconds after the first. This separation of space and time in classical physics indicates there is no coherent method to assign a single number representing the “distance” between two events in classical spacetime.
Do we truly inhabit Euclidean space? The answer is no. If spacetime were Euclidean, the Galilean transform would represent the correct relationships between coordinates of various reference frames, implying distances would be invariant across changes in reference frame. This is incorrect due to length contraction, prompting the question of the actual nature of the space we occupy.
Consider the collection of all spacetime points (x,y,z,t). Here, we will define the “distance” between two points in terms of the spacetime interval. If event A occurs at position (x?,y?,z?) and time t?, and event B at position (x?,y?,z?) at time t?, the “distance” between them is given by:

The function that calculates the spacetime interval between two events is known as the Minkowski metric, named after Herman Minkowski. Minkowski, who was one of Einstein's professors, formalized the concept of spacetime. Thus, rather than existing in a three-dimensional Euclidean space with an additional time dimension, we exist in four-dimensional Minkowski spacetime. The implications of this realization are significant and will be explored in a subsequent article. To conclude this article, let's address its most renowned consequence.
Demonstration: Mass-Energy Equivalence, E=mc²
One of the most recognized outcomes of special relativity is the equivalence of rest mass and energy. The rest mass of a particle is its mass as measured in the frame where the particle is stationary. This section aims to provide a rationale, though not a formal proof, for this assertion.
I will first argue based on physical principles that a particle can only travel at light speed if it possesses no rest mass. The actual proof will be deferred to the follow-up article, which will cover applications of relativistic physics.
Suppose a particle appears to travel at light speed in frame S, covering distance L in time ?t such that c?t = L, leading to (?s)² = (c?t)² - L² = 0. By the invariance of the spacetime interval, (?s')² = (?s)², thus in any other reference frame S', (?s')² = (c?t')² - (L')² = 0, yielding L'/?t' = c. This indicates that the particle maintains a speed of c in every inertial frame, implying it lacks a rest frame, rendering the concept of rest mass meaningless. This fulfills the "only if" part of the argument.
Now, if we assume there exists a frame where the particle is at rest and possesses zero mass, then this particle effectively does not exist: being at rest, it cannot transfer momentum to other particles, and with no mass, it cannot receive momentum from any other particle, thereby precluding any potential interaction with the universe. Since we only consider particles with meaningful existence, we can conclude that no frame exists where a massless particle is at rest, necessitating that all massless particles must travel at light speed. This satisfies the "if" part of the claim.
We will further explore in subsequent discussions how relativity alters our understanding of momentum and energy, though the fundamental conservation laws still hold: momentum and energy remain conserved within each reference frame.
A positron is a subatomic particle and the antimatter counterpart of the electron. It mirrors an electron in every aspect, save for its opposite charge. Experimentally, it has been observed that when a particle and its antiparticle collide, they annihilate, resulting in radiation. The expression for this process is:
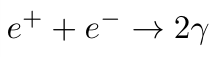
Where e? denotes a positron, e? signifies an electron, and ? represents a photon, with two photons being produced. Consider the situation where both the electron and positron are at rest and in contact just before annihilation. The total mass of the system is 2m?, double the mass of an electron, and the total momentum is zero. However, post-annihilation, the total rest mass drops to zero as the resultant photons travel at light speed. Where does the mass go, and where does the energy originate?
Since momentum is conserved, after annihilation, the total momentum remains zero, meaning both photons must possess equal magnitude p but move in opposite directions. Although photons lack rest mass, they still exhibit kinetic energy, expressible as E = pc.
Experimental results indicate that following annihilation, the combined kinetic energy of the two photons is approximately 1.637×10¹³ Joules. The total rest mass of two electrons is roughly 1.829×10?³ kilograms. When this total rest mass is multiplied by c², we find (2m?)c² = 1.644×10¹³ Joules, which aligns with the total energy released, allowing for rounding discrepancies. This energy-mass relationship holds true for similar experiments involving protons and antiprotons, neutrons and antineutrons, muons and antimuons, and beyond.
Given the conservation of energy, it follows that the energy present in the system prior to annihilation must equal that following the event. This leads us to hypothesize that the energy prior to annihilation was stored as the mass of the electron and positron, quantified as E = mc², with the annihilation process converting this energy into the kinetic energy of the photons. This explanation accounts for both the emergence of kinetic energy in a system that initially possessed none and the disappearance of rest mass, though we still need to substantiate this, which will be addressed in the next article.
Update April 20, 2020: The sequel is now available: Thinking Relativistically.
Conclusion and Copyright Information
Any images without citations are my original work. Some examples presented are inspired by those found in the textbook Modern Physics for Scientists and Engineers, 2nd edition by Taylor, Dubson, and Zafiratos.