Chapter 1: The Quest for Understanding

The exploration of our universe's origins poses significant challenges, particularly in explaining quantum phenomena. This piece investigates the notion that quantum events may have emerged from George Spencer-Brown’s Laws of Form. This framework is arguably one of the most fundamental bases for mathematics and epistemology, centering around the concept of a "Distinction." A Distinction effectively divides a domain, leading to a new understanding of mathematical singularities within Anti-de Sitter (AdS) space, as discussed in Article #7, which questions whether mathematics is foundational to reality.

> One interpretation of this is that the content along the boundaries of AdS space-time represents a cleavage in a domain.

Section 1.1: Spencer-Brown's Mathematical Framework

Spencer-Brown devised his mathematical theory while investigating efficient train routing. He categorized states into ‘marked’ and ‘unmarked’ by assigning values to specific states. For instance, as a train moves from one area to another, regions may shift from ‘unmarked’ to ‘marked’. As more complex routing scenarios arose, he discovered paradoxes in how these states interacted—specifically, that ‘marked’ regions had to relate back to ‘unmarked’ ones.

Consider a train tasked with picking up and dropping off packages in various regions. When the train enters a new region, its status changes from ‘Unmarked’ to ‘Marked’.

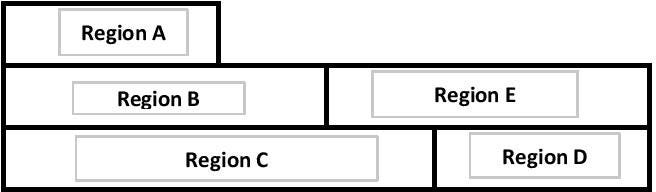
Initially, all regions start as ‘Unmarked’. As the train moves to Region B, it picks up a package for Region D. Subsequently, regions C and D also transition to ‘Marked’. However, upon returning to Region B, the rules dictate that it reverts back to ‘Unmarked’. This scenario illustrates how a single region can simultaneously embody both states.

Instead of viewing this as a contradiction, Spencer-Brown proposed that the system oscillates between these two states over time, introducing a temporal dimension to spatial considerations. In AdS boundaries, the acts of entering, emerging, and re-entering these boundaries represent a ‘self-reflexive act’ that introduces a time-like aspect to the AdS space.

Section 1.2: Expanding the Concept of Re-entry

Neuroscientist Francisco Varela expanded on Spencer-Brown's ideas, integrating the concept of re-entry into the system's foundational structure. This addition transforms the dichotomy of marked/unmarked (true/false) into a spectrum where a middle ground exists—represented by the color grey. Along with Humberto Maturana, Varela coined the term ‘autopoiesis’ to describe how biological systems self-organize, functioning autonomously while maintaining a complex structural openness.

The re-entry concept can be illustrated mathematically by a fractal equation, which recursively uses its output as input for subsequent iterations. Fractals exist in the complex space that bridges ordinary Euclidean dimensions, capturing how various forms—like coastlines and mountains—can be represented through self-similar patterns.

In AdS space, fractals describe how the bulk content is manifested at the boundary, which is both holographic and fractal in nature. As information re-enters boundaries, it becomes increasingly intricate, consistent with the quantum principle that “what can happen, does happen,” albeit often after numerous iterations.

Chapter 2: Quantum Phenomena and Mathematical Foundations

Applying Spencer-Brown’s Laws of Form to an AdS space with a Klein bottle topology illustrates how shapes transition between ‘upright’ and ‘upside down’. Once a shape rotates inside this topology, it produces two forms: one ‘upright’ and another ‘upside down’. This process can yield a fractal representation where a single shape embodies a history of identical forms compressed within a self-similar structure.

The three-dimensional AdS space with a Klein bottle topology introduces a fourth, time-like dimension. Professor Carlo Rovelli's Loop Quantum Gravity (LQG) theory posits that space is composed of mathematical entities called spin-foam, which are interconnected in diverse configurations. This framework suggests that historical information is embedded within the fabric of space-time, aligning with many concepts presented in this article.

The five Platonic solids exemplify geometric fractals, capable of fitting within and outside themselves infinitely while preserving self-similarity across scales. The growth of shapes in AdS space, influenced by their journeys through Klein bottles, can be measured by how many smaller shapes reside within a larger one, referred to as ‘scale’.

Mathematically, the scale of shapes can be expressed in terms of repetitions, revealing patterns akin to the Fibonacci sequence, which can also imply the emergence of a time-like dimension in AdS space.

The relevance of quantum phenomena to these discussions is underscored by recent work from Grangier and Auffeves, who argue that quantum randomness arises from contextual factors rather than merely a lack of information. Their framework suggests that quantum states are determined by the combined nature of systems and their contexts, offering a richer understanding of randomness.

In conclusion, the exploration of mathematical theories related to the origins of space, time, and quantum phenomena opens a dialogue on whether these phenomena can be logically explained through mathematical constructs.

For further reading, please visit the following resources: