Chapter 1: Introduction to the STEP Challenge

Navigating the complexities of Cambridge's STEP mathematics test can be daunting. In this guide, we will tackle a problem from the STEP 2 exam of 2019, which serves as an excellent illustration of how various mathematical concepts intertwine and challenge our intuition. Let's solve this together!

The Problem

Part (i)

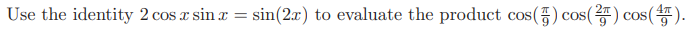
Initially, I approached the first section of the problem differently, but the underlying methods were fundamentally similar. Here’s the strategy I employed (note that we are not considering specific cases where sin x=0 in this approach).

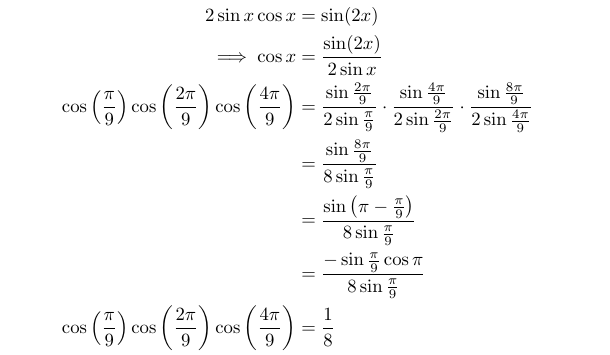
This provided a promising start! It's common for STEP questions to introduce the concepts gradually, with the initial part serving as a foundation for more complex ideas later on. Below are the solutions offered by Cambridge, which I personally find more appealing.

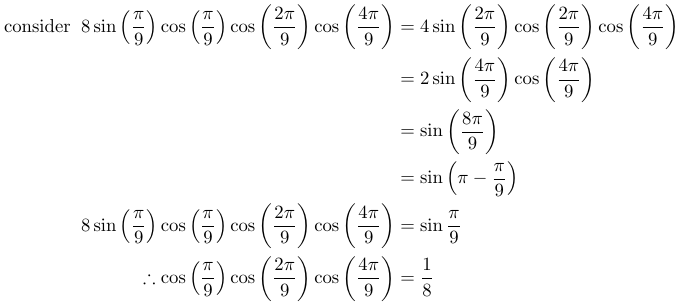
This method required recognizing the clever strategy of multiplying sin(x/9) with the cosine product, leading to a convenient cancellation.

Part (ii)

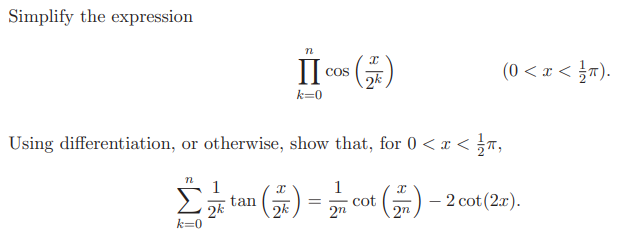
In this section, we are tasked with generalizing the product identified in Part (i). We could opt to multiply the entire product by sin(x/2^k) or follow my substitution method, which involves replacing cosine terms with sine terms using the double angle formula. I'll demonstrate my approach, but feel free to explore the alternative method.

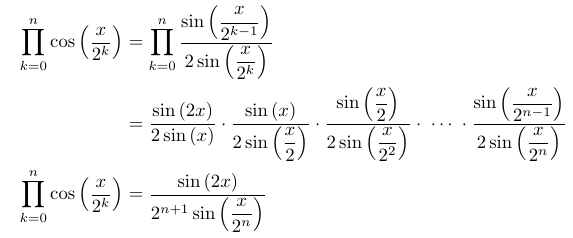
The next result posed a significant challenge for me in determining where to begin. I initially attempted to differentiate the provided result, which led to sec²x terms, but I soon found myself at an impasse. I was also deterred by the fact that the previous result was a product while we are now asked to demonstrate a summation. Unfortunately, I couldn't solve this part and had to consult the solutions for guidance. The key idea is to take the logarithm of both sides of the product. By utilizing logarithmic properties, we can transform the result into a summation of logarithmic terms, allowing us to differentiate. A helpful hint is in the question's mention of differentiation, suggesting that the integral of tan x relates to ln(cos x). (Also, recall that the question states we need not concern ourselves with convergence issues.)

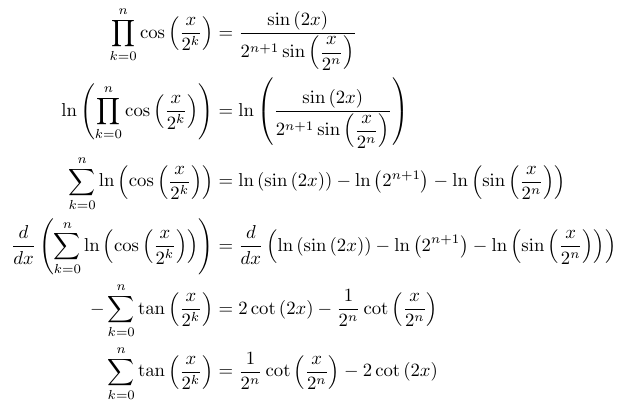
Once we recognized the need to take logarithms, the result unfolded beautifully. This serves as a valuable lesson for STEP problems and mathematics in general: always consider your destination and strategize your path towards it. Here, we transitioned from a product to a summation, and logarithms facilitated this transition.

Part (iii)

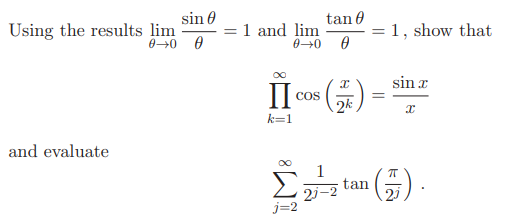
Finally, we are required to evaluate the infinite product and summation. The product result follows naturally from taking limits as n approaches infinity on both sides of our outcome from Part (ii). I will employ small angle approximations for sin x here, as the two limits at the start of Part (iii) encourage this approach.

The concluding result utilizes the tan summation derived in Part (ii). Note that here, x takes on a specific value, which we must also consider.

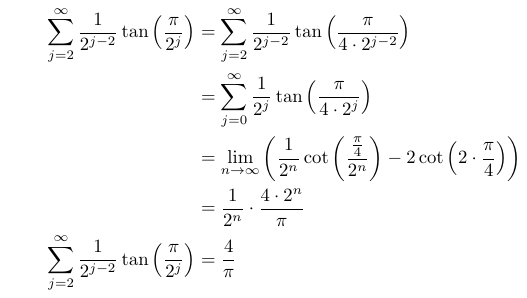
And that’s a wrap! I hope you found the journey of solving this problem enjoyable. This question exemplifies the importance of methodical thinking in mathematics; often, we must envision our endpoint and reverse-engineer our way there instead of starting from scratch.

Thank you for reading! I welcome any thoughts you may have on the problem.

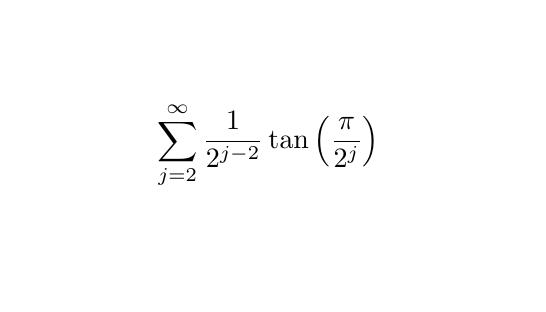
Chapter 2: Preparation for the Admissions Test

To further enhance your preparation for the Cambridge admissions test, consider the following resources:

This video titled "How to Do Well in the MAT Admission Test | Cambridge Students Advice" provides valuable insights and strategies to excel in the admissions process.

Another helpful video, "Should I do more than 3 A-levels? [Cambridge CS admissions]," discusses the implications of A-level choices for prospective Cambridge students.