Exploring the Mystifying Banach-Tarski Paradox in Mathematics
Written on
Chapter 1: The Enigma of the Banach-Tarski Paradox
Can a solid ball be split into a finite number of pieces that can be reassembled to create two identical copies of the original ball?
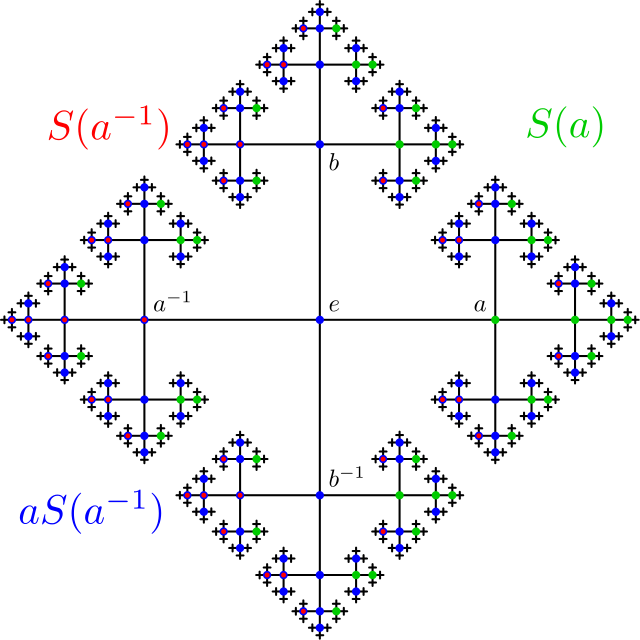
When I first encountered this concept, I nearly spilled my coffee. In mathematics, theorems are expected to be logical and provable. Thus, when faced with something as perplexing and counterintuitive as this, we must delve into the proof to grasp the underlying principles.
This article explores a result so astonishing that it has led some mathematicians to reconsider the fundamental principles of mathematics itself. Should we revise our entire mathematical framework to eliminate such peculiarities? Fortunately, the majority of us accept this result, even if it continues to baffle some.
Let’s dissect the paradox.
Section 1.1: The Paradox Unveiled
To grasp this phenomenon, we need to articulate some mathematical statements. First, let's introduce the renowned Banach-Tarski paradox. While its formal description involves group actions, we can summarize it informally as follows:
Theorem (Banach-Tarski)
Given a solid ball in three-dimensional space, it is possible to decompose the ball into a finite number of disjoint subsets, which can then be reassembled to create two identical copies of the original ball.
To clarify, this theorem implies that we can represent a ball as the set {(x, y, z) | (x - a)² + (y - b)² + (z - c)² ≤ r} for some center point (a, b, c) and radius r > 0. We can break this set down into a finite number of subsets (as few as five) such that if A and B are any two of the subsets with A ∩ B = ∅, the union of these subsets reconstructs the entire ball. By applying rotations and translations, we can create two new identical copies of the original ball.
Wait… Are you suggesting that we can produce two identical balls by merely partitioning the original and rearranging the pieces through rotations and translations, without stretching or adding any new points?
Yes, that is precisely my assertion!
This seems impossible because these transformations typically preserve volume in our everyday understanding of solid objects. After all, we cannot slice an orange into five pieces and reassemble it to yield two oranges, each retaining the original mass, right? That would imply the creation of mass/energy from nothing, which is unthinkable for physical objects.
So, what’s happening here?
Section 1.2: Mathematical Interpretation
To unravel this, we must examine the concept of volume from a mathematical perspective. Volume does not apply universally to all sets. For a standard ball in three-dimensional space, we can easily define volume. However, what about arbitrary subsets of ℝ³? It turns out that for some sets, volume cannot be defined.
To investigate this, we turn to measure theory, which serves as the cornerstone of modern probability and integral theory. This framework allows us to determine which sets can be “measured.” Specifically, if a set is Lebesgue measurable, we can assign a volume to it.
The subsets into which the ball is divided are not the standard pieces you might expect from cutting a cake! In fact, these subsets are not even measurable, meaning our intuition about volume-preserving transformations does not apply since these subsets lack a volume, even in an abstract sense.
So, what are these subsets? Well, explaining this without delving into group theory is quite challenging. They certainly defy visualization. The proof relies on ingeniously constructed infinite sets that can be transformed into one another through rotations around two independent axes.
The precise characterization of these subsets and the proof of the paradox are beyond this article's scope, but it involves a group known as "the free group in two generators," along with an isomorphism linking that group to a rotation group in three-dimensional space. By identifying a “paradoxical decomposition” of this free group, we can translate it into a geometric representation in three-dimensional space!
Chapter 2: Questioning Mathematical Foundations
At the outset, I mentioned that this paradox has prompted some mathematicians to reevaluate the very foundations of mathematics. This stems from deep philosophical inquiries into the nature of mathematical reasoning.
A theorem, which is simply a verified mathematical truth, is established using other truths, which in turn are also proven through other truths. This cycle must eventually terminate, and it does so at a set of foundational “truths” known as axioms. Axioms cannot be proven; they are assumed to be true. Naturally, we require these axioms to be somewhat self-evident since basing mathematics on fallacies would enable us to prove fallacies as well.
Modern mathematics generally rests on the Zermelo-Fraenkel set theory, abbreviated as ZFC, formulated in the early 20th century. The "C" refers to the axiom of choice, which has historically stirred controversy. An informal version states that given any collection of sets, each containing at least one element, we can select exactly one element from each set, even if the collection is infinite.
This seems reasonable, right? So what’s the catch?
The issue arises when dealing with infinite sets without an explicit function to facilitate selection, leading us to assume the existence of such a function, even when it necessitates uncountable choices. If we cannot make explicit selections, how can we be sure the resulting set of “choices” exists? This has profound implications for all of mathematics.
It has been demonstrated that the axiom of choice is independent of the Zermelo-Fraenkel axioms, allowing us to explore mathematics based solely on the ZF axioms and perhaps a milder version of AC. In their original 1924 paper, Stefan Banach and Alfred Tarski employed the axiom of choice to establish the paradoxical decomposition that underpins the proof. Later, it was shown that the Banach-Tarski paradox cannot be proven solely with Zermelo-Fraenkel axioms.
In 1991, Janusz Pawlikowski proved that while the Banach-Tarski paradox surpasses ZF, it is less robust than full ZFC. Specifically, a weaker version of the axiom of choice known as the ultrafilter lemma suffices, in conjunction with the Zermelo-Fraenkel system, to demonstrate the Banach-Tarski paradox. This indicates that the paradox does not strictly require the axiom of choice, although its proof is more elegant when that axiom is permitted.
Final Thoughts
The Banach-Tarski paradox is captivating as it delves deep into the foundations of mathematics and challenges our intuitive grasp of geometric concepts. The apparent paradox (which is, in fact, a theorem) arises from the ability to partition a well-defined volume (measure) into finite subsets that lack volumes. Thus, when we recombine them into a set with a volume, we should not expect it to retain the same volume as the original set.
Moreover, a stronger version of the theorem suggests that given any two solid objects, regardless of their sizes, the pieces from either can be reassembled into the other. This notion is sometimes whimsically phrased as "a pea can be chopped up and reassembled into the Sun," leading to the pea and Sun paradox.
A detailed exploration of the Banach-Tarski Paradox, illustrating its implications in mathematics.
An in-depth analysis of the Banach-Tarski paradox, discussing its historical context and relevance in modern mathematics.