The Mystery of the Fifth Postulate

Euclid's fifth postulate, unlike the first four, generated immediate intrigue and controversy among mathematicians. For centuries, this seemingly intricate statement posed a challenge, inviting scrutiny from some of the greatest mathematical minds.

In contrast to the straightforward nature of the other postulates, the fifth was neither simple nor intuitively clear, leading to widespread speculation that it might be a theorem in disguise, awaiting proof from the other four postulates.

Greek philosopher Proclus was among the first to express skepticism regarding the fifth postulate, suggesting it should be removed from the list of postulates altogether. He contended that if it were truly fundamental, it ought to be demonstrable from the first four postulates.

This sentiment reverberated throughout academia for over two millennia as numerous mathematicians sought to validate the fifth postulate using only the first four. Notable figures like Ptolemy and Proclus claimed to have succeeded, yet they merely reformulated the fifth postulate in different terms.

The Parallel Postulate essentially asserts that for any given line, there exists only one parallel line that can pass through a point not on the initial line. The pursuit of proof for this postulate led to various reformulations.

One attempt restated it as: For a given line and a point not on it, there exists a unique line through the point that is parallel to the original line. However, this rephrasing did not simplify the problem or yield the desired proof.

In an effort to resolve the conundrum, some mathematicians, including the renowned al-Haytham and Omar Khayyam, employed an alternative method known as proof by contradiction. They retained the first four postulates but assumed the fifth to be false.

The aim was to use these adjusted postulates to derive theorems and seek contradictions. If a contradiction emerged, it would imply that the newly defined fifth postulate was wrong, thereby validating Euclid's original postulate by default.

This approach led to two alternative considerations regarding Euclid's Parallel Postulate. The first suggested that no parallel lines could be drawn through a point not on a line. This idea was swiftly dismissed, as it contradicted the second postulate, which permits the indefinite extension of lines.

The second option posited that multiple parallel lines could pass through the specified point. However, this approach also failed to produce the anticipated contradiction.

Despite centuries of relentless effort and creativity, every attempt to prove the fifth postulate ultimately fell short. The persistent inability to validate it as a theorem gave rise to an intriguing possibility: perhaps the postulate was indeed independent of the others, a notion that would eventually lead to entirely new geometric concepts.

Bolyai’s Hyperbolic Geometry

The stalemate in proving Euclid's fifth postulate resulted in a significant breakthrough in the early 19th century, thanks to Hungarian mathematician János Bolyai.

As a young man, Bolyai became deeply fascinated with the fifth postulate, dedicating countless hours to deciphering its complexities. Despite warnings from his father, Farkas Bolyai, a respected mathematician who had also struggled with the postulate, János persevered.

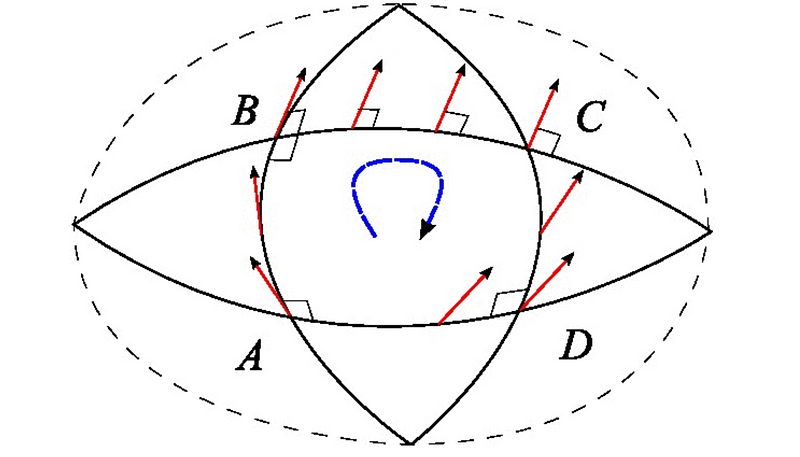
Bolyai's approach was revolutionary. He entertained the possibility that the fifth postulate was not a theorem that required proof but rather an independent statement. This led him to investigate a realm where multiple parallel lines could exist through a point not situated on a given line. His exploration of this idea marked the inception of hyperbolic geometry, a groundbreaking new branch of mathematics.

In hyperbolic geometry, the conventional understanding of parallel lines underwent a radical transformation. Bolyai envisioned a surface where, unlike a flat plane, numerous lines could run parallel to a given line without ever intersecting it. This concept defied traditional geometric understanding and necessitated a rethinking of spatial relationships.

Bolyai's breakthrough came when he realized that the definitions of 'straight' and 'parallel' could be reconceptualized on curved surfaces. He discovered that the shortest path between two points on a curved surface, known as a geodesic, could function as a 'straight line' in this new geometric framework. This represented a significant departure from the flat, two-dimensional plane of Euclidean geometry.

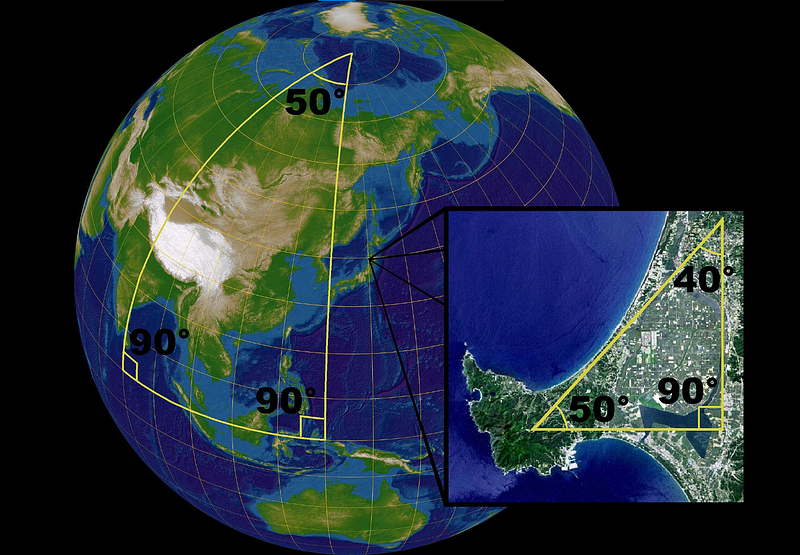
The concept of geodesics was further clarified through the example of air travel. Airplanes, aiming to cover the shortest distance, follow paths that appear curved on maps due to the Earth's curvature. These routes are, in reality, geodesics or the 'straightest' paths across the spherical surface of the Earth.

Although Bolyai's work on hyperbolic geometry was groundbreaking, he faced challenges in gaining recognition. In 1832, he published his findings as an appendix to his father's textbook. Carl Friedrich Gauss, a prominent mathematician of the time, acknowledged the brilliance of Bolyai's work but admitted to having reached similar conclusions independently years earlier, though he never published his findings. This revelation did not deter Bolyai, who continued to develop his ideas, making significant contributions to the field of geometry.

The birth of hyperbolic geometry by Bolyai laid the groundwork for a deeper understanding of space and geometry. It challenged the long-held beliefs of Euclidean geometry and opened avenues for future mathematicians to explore and expand upon these revolutionary concepts, leading to substantial advancements in our understanding of the universe.

Parallel Worlds

János Bolyai's groundbreaking contributions to hyperbolic geometry heralded a new era in mathematics—one of non-Euclidean geometry.

This field represented a considerable departure from the well-established principles of Euclidean geometry, which had dominated mathematical thought for more than two millennia. The notion of non-Euclidean geometry contested the universal applicability of Euclid's fifth postulate and introduced the idea that diverse geometric truths could exist under various sets of postulates.

At the core of non-Euclidean geometry lies the assertion that the parallel postulate, as posited by Euclid, is not a necessity but one of several possible truths. While Euclidean geometry maintains that only one parallel line can be drawn through a point, non-Euclidean geometry contemplates alternative realities.

In one variant, known as hyperbolic geometry, an infinite number of parallel lines can pass through such a point. Conversely, in a different variant called spherical geometry, no parallel lines exist at all.

Carl Friedrich Gauss, often hailed as one of history's greatest mathematicians, also delved into the realm of non-Euclidean geometry independently. Around the same time as Bolyai, Gauss was investigating similar concepts but opted not to publish his findings, perhaps due to the controversial nature of challenging a two-thousand-year-old mathematical doctrine. Nonetheless, his private correspondence revealed his profound engagement with these radical ideas.

The development of non-Euclidean geometry had profound implications for our understanding of space and the universe. It opened the door to the notion that the space we inhabit might not adhere to the rules of Euclidean geometry. This revolutionary thought suggested that the universe could be curved or possess different geometric properties at various scales or in different regions.

The emergence of non-Euclidean geometry also laid the foundation for further advancements in mathematics and physics. It marked a crucial step toward the formulation of modern theories of space, time, and gravity.

Riemann’s Curvature

Following the groundwork established by Bolyai and Gauss in non-Euclidean geometry, German mathematician Bernhard Riemann introduced a revolutionary concept that would broaden the understanding of geometry even further.

Riemann, building on the ideas of his predecessors, introduced the notion of varying curvature, which permitted a more comprehensive description of different geometrical spaces. This idea represented a significant advancement, suggesting that the properties of space could vary from one location to another.

Riemann's concept of curvature was a fundamental shift from the flat planes of Euclidean geometry and the consistent curvature observed in spherical or hyperbolic geometries. Instead, he proposed a model where space itself could curve in various ways at different points, resulting in a geometry that was not uniform.

This approach allowed for the consideration of spaces that could be flat in some areas while curved in others, providing a more adaptable framework for comprehending complex geometrical structures.

The implications of Riemann's work were extensive and far-reaching. His insights regarding curvature equipped mathematicians and physicists with the tools needed to describe and analyze the properties of various surfaces and spaces, including those that could not be easily visualized. Riemannian geometry became an essential tool for exploring and modeling a wide range of physical phenomena.

One of the most significant applications of Riemann's ideas emerged in the fields of astrophysics and cosmology. His concept of varying curvature was instrumental in developing theories about the universe's structure and shape. It provided a mathematical basis for understanding how large masses, such as stars and galaxies, could curve space, leading to new theories about gravity and the motion of celestial bodies.

Riemann's work on curvature also paved the way for Albert Einstein's renowned Theory of Relativity. Einstein utilized the principles of Riemannian geometry to illustrate how the presence of mass and energy could warp the fabric of space-time, resulting in the gravitational effects we observe. This marked a groundbreaking shift in our understanding of gravity, moving away from the notion of a force acting at a distance to a model where mass and energy shape the geometry of the universe itself.

From Geometry to Cosmology

The revolutionary concepts in geometry, particularly those regarding the curvature of space as articulated by Riemann, set the stage for one of the most significant breakthroughs in physics: Albert Einstein's theory of General Relativity. Einstein, a theoretical physicist, employed the principles of non-Euclidean geometry to fundamentally redefine our understanding of gravity and the universe's structure.

Einstein's journey toward formulating the General Theory of Relativity began with his 1905 Special Theory of Relativity. This initial theory established that physical laws remain consistent for all observers not experiencing acceleration, positing that the speed of light remains constant in a vacuum, irrespective of the movement of the light source or the observer. Although groundbreaking, the Special Theory focused primarily on objects traveling at constant velocities in linear paths and did not address the effects of gravity.

In 1915, Einstein expanded these ideas with the General Theory of Relativity, which confronted the issues of acceleration and gravity. Central to this theory was the proposal that massive objects such as planets and stars could warp the fabric of space-time surrounding them. This curvature of space-time—directly applying Riemann's concepts of varied curvature—became what we perceive as gravity.

Einstein's theory marked a radical departure from Newton's view of gravity, which conceptualized it as a force acting at a distance between masses. Instead, General Relativity posits that objects traverse the curved paths of space-time created by mass and energy. This new perspective elucidated why planets orbit the sun—not because of an invisible force acting between them, but because the sun's mass curves the space-time around it, creating paths along which the planets navigate.

The General Theory of Relativity revolutionized our understanding of gravity and significantly impacted cosmology, the study of the universe in its entirety. It provided a framework for grasping how the universe's composition could be influenced by the distribution of energy and mass.

Einstein's theory yielded predictions about phenomena such as light's curvature due to gravity, known as gravitational lensing, and led to the discovery of black holes—regions in space where gravitational forces are so intense that nothing, including light, can escape.

Einstein's theory was empirically tested during a solar eclipse in 1919 when observations confirmed that light from distant stars bent as it passed near the sun, exactly as General Relativity predicted. This confirmation was a pivotal moment in the history of physics, solidifying Einstein's theory as a cornerstone of modern science.

The Cosmic Puzzle

The investigation into the universe's shape is a significant endeavor in cosmology, deeply rooted in the principles of geometry and relativity. Determining the universe's shape requires understanding its curvature on a grand scale, extending the concepts of Euclidean and non-Euclidean geometries into the vastness of space.

Central to this exploration is the inquiry into whether the universe is flat, spherical, or hyperbolic in its overall geometry. This distinction is crucial, as it informs our understanding of the universe's origin, current state, and ultimate fate. In a flat universe, the rules of Euclidean geometry apply, and parallel lines remain parallel at infinite distances. In a spherical universe, parallel lines eventually converge, while in a hyperbolic universe, they diverge.

To ascertain the universe's shape, scientists employ precise measurements of cosmic phenomena. One of the key tools in this pursuit is the observation of the Cosmic Microwave Background (CMB), the residual thermal radiation from the Big Bang. The CMB serves as a cosmic backdrop, enabling scientists to measure the universe's geometry by analyzing the size and distribution of structures within it.

Recent data from space observatories like the Planck satellite have provided detailed measurements of the CMB. These observations are utilized to create a cosmic map that reveals the temperature fluctuation distribution across the sky. By analyzing these fluctuations, cosmologists can infer the large-scale geometry of the universe.

The latest findings indicate that the universe is remarkably flat, closely aligning with the principles of Euclidean geometry. This conclusion is based on measurements of the angles of triangles formed by light paths in the universe. In a flat universe, the angles of a large-scale triangle would sum to 180 degrees, consistent with observations of the CMB.

This understanding of the universe's flatness has profound implications. It suggests that the total energy density of the universe is near a critical value that separates a closed, spherical universe from an open, hyperbolic one. This critical density encompasses contributions from all forms of matter and energy, including the enigmatic dark matter and dark energy.

Euclid’s Enduring Legacy

The journey from the elemental lines of Euclid's "Elements" to the vast cosmos reflects the remarkable evolution of human thought in mathematics and physics.

Euclid's Postulates, once regarded as indisputable truths, paved the way for the revolutionary ideas of Bolyai, Riemann, and Einstein, reshaping our comprehension of the universe. The development of non-Euclidean geometry and the subsequent emergence of Einstein's theory of General Relativity exemplify the power of questioning and reimagining established concepts.

Today, our perception of the universe is significantly influenced by these groundbreaking ideas. The possibility that the universe may be flat, as suggested by studies of the Cosmic Microwave Background, provides profound insight into the nature of our cosmos. It illustrates a universe governed by principles that transcend everyday experiences, where the curvature of space dictates the motion of galaxies and the trajectory of light itself.