Exploring the Geometry of General Relativity and Its Implications
Written on
Chapter 1: Understanding Spacetime
What exactly is spacetime, and what mathematical tools are necessary to comprehend it? The framework of General Relativity, established by Albert Einstein, serves as our most effective model for understanding gravity. This theory heavily relies on geometry, leading to the development of an entire branch of mathematics known as differential geometry, which focuses on the geometrical foundations of general relativity. During my academic journey, I found the mathematical prerequisites quite demanding, primarily revolving around the calculus of curved spaces.

Despite the challenges, the effort to master this mathematics was worthwhile. General Relativity expands upon the principles of Special Relativity, offering a wealth of predictions that modern technology can test. For instance, it has accurately forecasted the existence of phenomena such as black holes, gravitational lensing, and gravitational waves. In this article, I aim to elucidate some fundamental mathematical constructs in General Relativity and illustrate how one might conceptualize a black hole within this framework.
Section 1.1: Flat Versus Curved Spacetime
In classical physics, time is treated as a constant, a ticking parameter that progresses steadily as physical events unfold—much like a clockwork mechanism. Conversely, General Relativity, akin to Special Relativity, treats space and time on equal grounds. It views time as just another coordinate, similar to how we describe spatial dimensions. The physical 'stage' where these interactions occur is termed spacetime. In both forms of relativity, we solve equations within this combined spacetime framework to analyze the motion of objects influenced by various forces.
However, there is a key distinction between General and Special Relativity. In Special Relativity, spacetime is regarded as flat. To grasp the concept of 'flatness' in spacetime, consider a simplistic analogy: envision a one-dimensional ant traversing a straight line over time. By placing space and time on an equal plane, we can depict the ant's trajectory using a spacetime diagram, where the y-axis represents time and the x-axis indicates the ant's position.
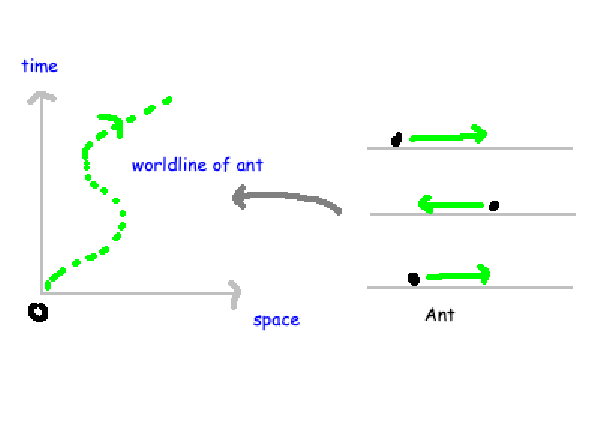
This path, known as a worldline, illustrates the ant’s journey in a two-dimensional representation. Physicists refer to this space as '1+1' since it comprises two dimensions. If we extend this concept to our three-dimensional world with one time dimension, it becomes a '1+3' space. This spacetime diagram is philosophically akin to a two-dimensional coordinate system on a flat sheet of paper, hence referred to as flat spacetime. This concept is pivotal to Special Relativity.
However, matters become more intricate when we consider curved spaces. A straightforward example involves an ant moving along the circumference of a circle. Although mathematically treated as a one-dimensional object, specifying its position requires one coordinate—the angle corresponding to its location on the circle.
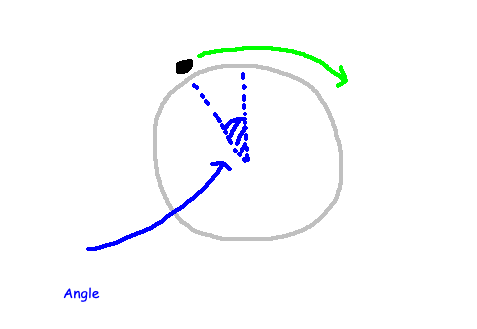
If we visualize the ant's movement over time, the resulting spacetime resembles a cylinder rather than a flat plane, constrained by the circular geometry. Consequently, we must approach the concepts of distance and change with greater care, as the geometry of a circle is more complex than that of a straight line.
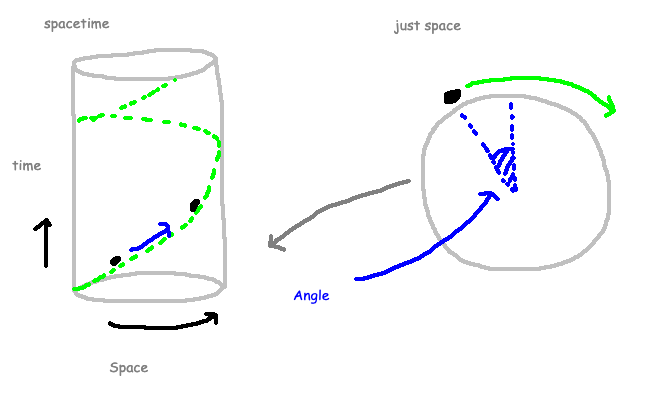
Empirical evidence reveals that our universe's spacetime is not flat but exhibits curvature. Thus, to refine our models, we must develop mathematical tools to address the complexities of curved geometries. This distinction embodies the essence of what separates Special and General Relativity.
Section 1.2: The Concept of a Metric
At the heart of General Relativity lies the metric. A metric is a mathematical construct that defines the distance between two points in space. In two-dimensional space, for example, we can measure the distance using Pythagoras' theorem if we know the coordinates of the two points. Similarly, in three-dimensional space, this theorem can be extended to measure distances.
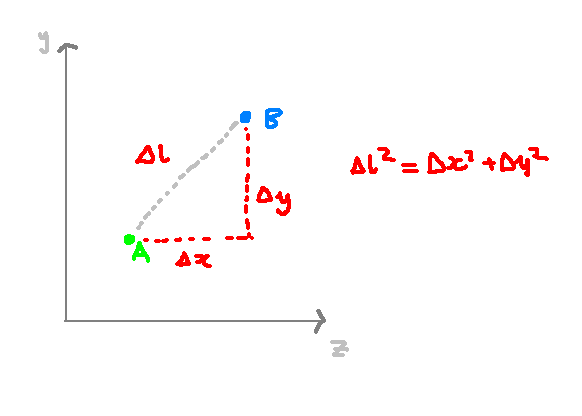
While the Euclidean metric, derived from Pythagoras' theorem, is commonly used, it is not the only metric available. Various metrics exist, each serving different purposes depending on the context. For instance, in a two-dimensional plane, one might use the sum of absolute distances in the x and y directions, known as the l¹ Norm.
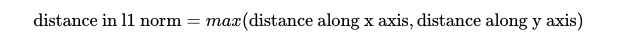
Mathematicians adhere to certain loose rules, or axioms, that define a valid metric. These intuitive principles include:
- If two objects have zero distance between them, they must be identical.
- The distance from object A to object B is equivalent to the distance from object B to object A.
- The distance from A to C cannot be less than the sum of distances from A to B and B to C.
Metrics also help quantify the magnitude of objects. For example, in physics, the velocity of a particle is often described with a vector, which has directional components. The absolute size of this vector is determined using a metric, where the size of the velocity vector equates to speed, devoid of direction.
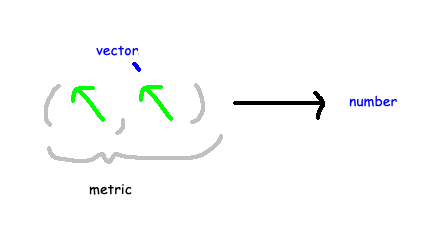
In conventional physics, the Euclidean metric is typically employed, suitable for flat spaces. However, General Relativity necessitates non-Euclidean metrics to accurately represent distances and sizes in curved spaces. Consequently, we must devise a straightforward method to express these metrics.
Chapter 2: Expressing Metrics in Curved Spacetime
When dealing with curved surfaces, writing down the metric becomes more complex. For flat metrics, physicists utilize the notation 'd' to denote small changes. Thanks to Pythagoras' theorem, a flat metric can be expressed as the sum of squares of small changes across each direction, incorporating time with a negative sign.
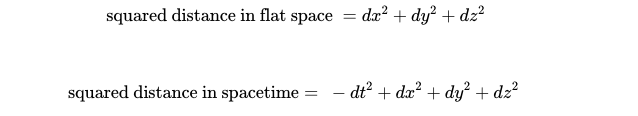
Transitioning to curved spacetime, we must identify two coordinates—latitude and longitude—to describe a point on a sphere. The corresponding metric can also be expressed through small changes in these coordinates.
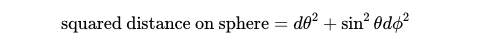
Time can similarly be integrated. According to Einstein's General Relativity, permissible metrics must comply with a set of equations known as Einstein's field equations. One such valid metric pertains to black holes, referred to as the Schwarzschild metric, represented by a complex expression.
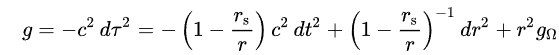
Utilizing this metric allows us to derive numerous properties of black holes. For instance, we can demonstrate that objects near a black hole's center cannot escape its grasp, that light can bend around a black hole, and that time flows more slowly for those closer to a black hole compared to an external observer.
Gravity is Geometry (General Relativity) - YouTube
This video delves into how gravity is fundamentally a geometrical phenomenon, explaining core concepts of General Relativity.
Shing-Tung Yau - Geometry of spacetime and mass in general relativity - YouTube
Explore the intricate relationship between geometry, spacetime, and mass as outlined by Shing-Tung Yau in this insightful presentation.
Wrap Up
I hope this introduction provides valuable insights into the concepts surrounding relativistic physics. Stay tuned for further explorations!