Section 1.1: Understanding Fuel Efficiency Calculation

Imagine a vehicle traveling 1 mile at a speed of 45 mph. You might wonder why this requires energy at all. The answer lies in air drag. As the vehicle moves, it encounters resistance from the air, creating a backward force. This force, when exerted over the distance of 1 mile, performs negative work (in physics terms) because it acts opposite to the direction of motion. For a constant force, work is calculated as follows:

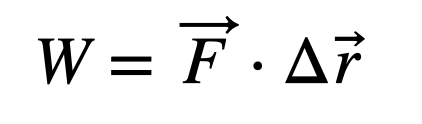
Here, F represents the force vector, and ?r signifies the displacement vector. The dot indicates the dot product. Given that this force opposes motion, F and ?r are oriented 180 degrees apart. Consequently, the work done against air drag is given by -F*?r.

Next, we must consider the force generated by air resistance. If you extend your hand outside a moving vehicle's window, you can feel this force. By experimenting, you'll observe that its magnitude depends on several factors:

• The speed of the vehicle (v).
• The size of your hand (area = A).
• The aerodynamic shape of your hand, which affects the drag coefficient (C).

Another influencing factor is air density (?), though this is less tangible as it’s difficult to alter air density in practice.

Given these variables, one model for calculating the magnitude of the air drag force can be expressed as:

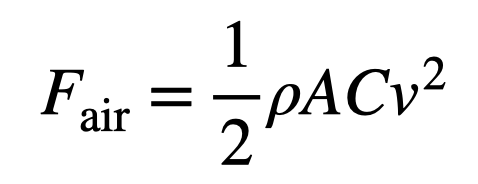
Don’t worry about the factor of “1/2” — if it aligns with empirical data, that’s acceptable. Other models for drag force exist, but this one is referenced in the book. Consequently, the work done by air is:

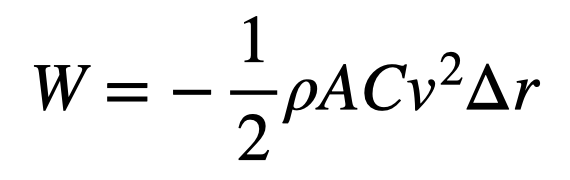
To maintain the car's total kinetic energy, there must be a corresponding decrease in the chemical potential energy from burning gasoline. So, how much energy do we obtain from gasoline? As noted in the book, gasoline has an energy density of 34.2 MJ/L — that’s 34.2 million Joules per liter. We can explore units later.

For now, let’s express the decrease in usable chemical energy as:

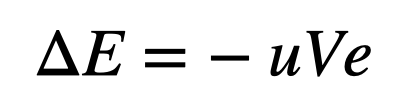
In this equation, u stands for energy density, V is the volume of gasoline, and e represents efficiency — the proportion of energy that contributes to useful work. Since the change in energy must equal the work performed by air drag, we can equate these two expressions:

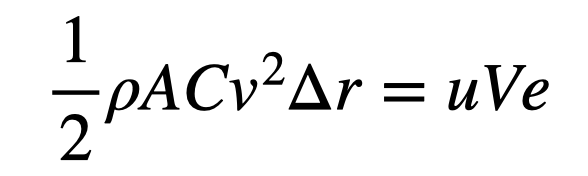
Next, let’s clarify “miles per gallon.” This simply refers to the units involved, where we ultimately want displacement divided by volume.

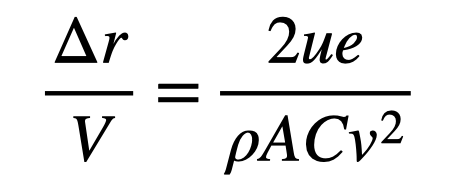
This aligns closely with what is presented in How To, although they use “energy density” in the numerator, which should actually be “effective energy density.” Nonetheless, it is largely accurate.

Section 1.2: Checking the Units

Before diving into numerical results, let’s review the units. If I include the units on the right side of the equation from the book, I get:

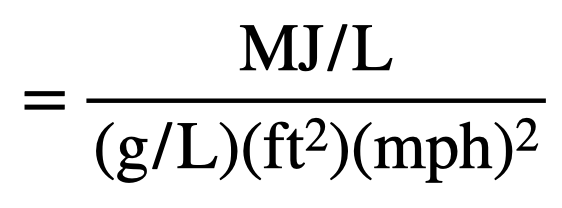
This equation is quite messy, combining both Imperial and metric units, with distances expressed in both miles and feet.

So, what are the best units to employ here? In SI base units, each variable should be represented as follows:

• Energy density = Joules/m³
• Efficiency = dimensionless (percentage)
• Air density = kg/m³
• Cross-sectional area = m²
• Drag coefficient = dimensionless
• Velocity = m/s

Utilizing these units, the fuel efficiency will be expressed in units of 1/m², which seems odd, but miles per gallon also has similar dimensional characteristics.

Section 1.3: Numerical Analysis

Now we are ready to crunch some numbers. I’ll begin by plugging in the values as presented in the book. Of course, I used Python for this calculation, yielding:

It doesn't match the 0.8 mpg stated in the book, which is expected due to the incorrect units. By correcting the units to SI, the output appears as:

From this, I obtain a fuel efficiency of:

Expressed in units of 1/m², or perhaps more appropriately as meters per cubic meter of gasoline. Let’s convert this into km/L for better comprehension. Remember, the key to unit conversion is to “multiply by 1.” Here’s how I’ll represent the current units as m/m³.

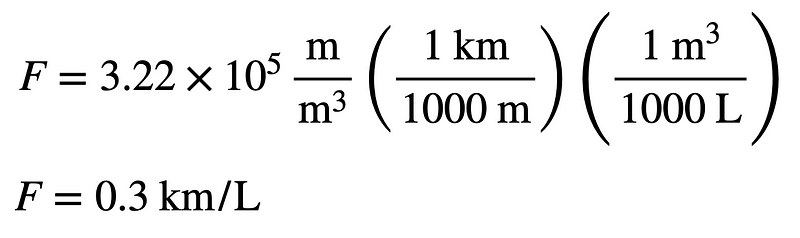
By multiplying my value by 1 km/1000 m, it keeps the integrity of the units since 1 km equals 1000 m. This gives me a fuel efficiency expressed in a more familiar unit. If you convert this to miles per gallon (I'll leave this calculation for you to complete as an exercise), you’ll find it to be approximately 0.706 mpg, which is close to the figure indicated in the book.