# Comparing Google Gemini and Bing's GPT-4 through AMC 12 Problems
Written on
Chapter 1: Introduction to the AI Showdown
Earlier this year, I published a piece evaluating the problem-solving capabilities of Google's Bard in contrast to ChatGPT. The conclusion was that while GPT-4 maintained a superior edge, Bard had shown commendable advancement.
Now, with Google having introduced the Gemini model and boldly asserting its superiority over GPT-4, it’s time to re-examine this direct competition.
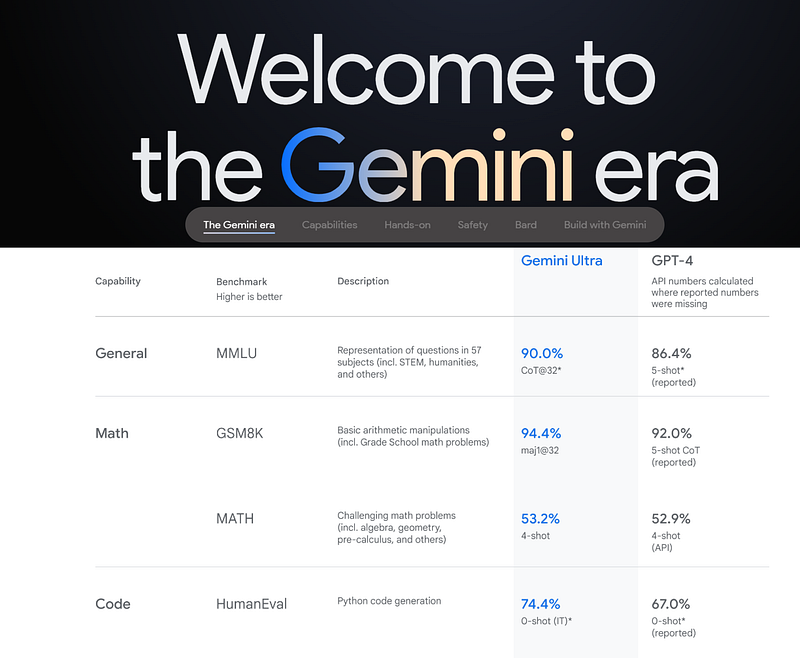
Why the 2023 AMC?
The American Mathematics Competition (AMC) provides an excellent array of math problems aimed at assessing genuine understanding rather than mere memorization or mechanical application of formulas. The AMC served as one of the sources for the MATH dataset utilized to benchmark both GPT-4 and Gemini.
In addition, the GSM8K dataset, which features more straightforward math problems designed specifically for AI training, tends to be more repetitive and formulaic. Conversely, the AMC problems, crafted by professional mathematicians and educators, offer greater variety and depth, thus serving as a more effective benchmark for evaluating true intelligence and problem-solving skills.
Notably, the 2023 AMC problems were released in November 2023, shortly before the Gemini launch, making it highly improbable that these specific problems were included in Gemini's training data.
Now, let’s dive into the analysis!
Chapter 2: AMC 12A Problem Evaluations
Problem 1: A Speed-Distance-Time Question
We’ll kick things off with a relatively straightforward problem from the 2023 AMC 12A:

For all problems, I utilized the same prompt: “Show me how to solve this math problem,” followed by the copied image.
Initially, Gemini expressed enthusiasm about its improvements in tackling word problems. It began well by defining appropriate variables and attempting to formulate a system of equations.
However, it faltered by reusing the same variable for different distances and ultimately claimed “no solution” when solving the equations.
Bing (utilizing GPT-4) adopted a more accurate approach, although it made a significant arithmetic error: 45 ÷ (18 + 12) equals 1.5, not 1.875. It’s puzzling that while GPT-4 can excel in writing essays, it struggles with basic arithmetic.
Though both AIs failed to arrive at the correct answer, Bing's approach was closer and methodologically superior.
Score: Bing: 1 vs Bard: 0
Problem 3: Counting Perfect Squares
This number theory problem should also be relatively simple.

Bard initially provided a correct answer—8 perfect squares—but then veered off course with flawed reasoning, arriving at an incorrect total of 76, which was neither accurate nor among the multiple-choice options. Strangely, Bard recognized this as an AMC 12 problem and linked to an unrelated AMC problem from 2007.
Bing exhibited a similar tendency, albeit with a different method that included multiple errors. It also referenced a 2007 problem related to perfect squares, yet failed to utilize the solution effectively.
Bard deserves credit for its correct initial attempt, so I’m awarding this point to Bard.
Score: Bing: 1 vs Bard: 1
Problem 4: Counting Digits
Next, we tackle a problem focused on counting digits in a large number.

Unfortunately, Bard misread the image, failing to differentiate between the exponents and the base numbers, despite its claim of being "multi-modal" from the outset.
Bing correctly interpreted the exponents but made its own image-detection error, mistaking the last power of 5 for a power of 3. It also misapplied index laws, though it attempted the right method.
In this round, Bing takes the point.
Score: Bing: 2 vs Bard: 1
Problem 9: Geometry Challenge
Moving on to a geometry problem, let’s see if Gemini’s multi-modal capabilities help here.
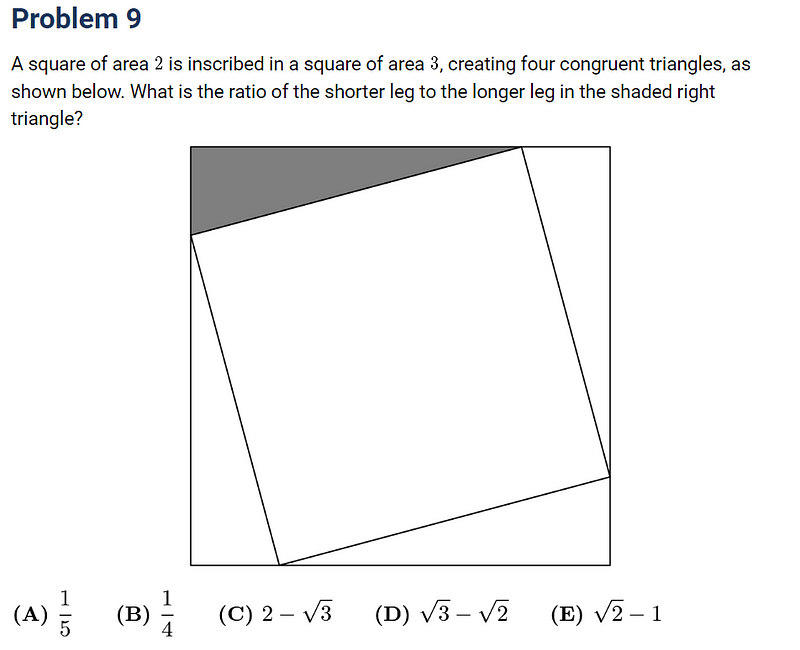
Unfortunately, Gemini misinterpreted the text again, confusing a “3” with a “v.” Despite this transcription issue, it recognized that the Pythagorean theorem was the appropriate method for solving the problem.
Bing also understood to apply the Pythagorean theorem but mixed up the sides of the triangle.
Both AIs were on the right path but ultimately could not solve the problem. I’ll give them each a point.
Score: Bing: 3 vs Bard: 2
Problem 10: Algebraic Equations
Lastly, we’ll look at a pair of non-linear equations, a task that has long been manageable for Mathematica.
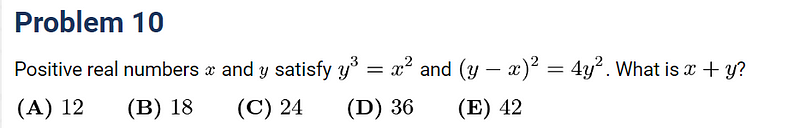
Regrettably, both AI models misinterpreted the written math. I provided LaTeX input to see if they could solve the equations correctly.
Gemini performed poorly here, and Bing and GPT-4 did not fare any better. Thus, no points will be awarded for this round.
Score: Bing: 3 vs Bard: 2
Problem 20: Modified Pascal’s Triangle
By this point, I had limited expectations, but I was curious to see how they would handle a non-traditional problem involving a variation of Pascal’s Triangle.

Bard surprisingly answered a completely unrelated question, which was quite disappointing given Google’s extensive marketing of Gemini.
In contrast, Bing successfully identified this as a problem from the 2013 AMC 12A! However, it still provided an incorrect solution.
Despite the errors, Bing deserves the point for its recognition of the problem.
Score: Bing: 4 vs Bard: 2
Conclusion
It’s clear that OpenAI and Microsoft maintain the lead in solving mathematical problems. To be fair, Bard is currently operating with the Gemini Pro model, while the more powerful Gemini Ultra model has yet to be released. I plan to revisit this comparison next year, likely in conjunction with GPT-5's capabilities.
AGI Will Not Take All Our Jobs
But it will change all our jobs.