Chapter 1: Introduction to Tangent Lines

What is the angle between these two tangent lines? This intriguing calculus question invites you to ponder before diving into the details. The problem originates from Sylvanus Thompson’s Calculus Made Easy (page 86).

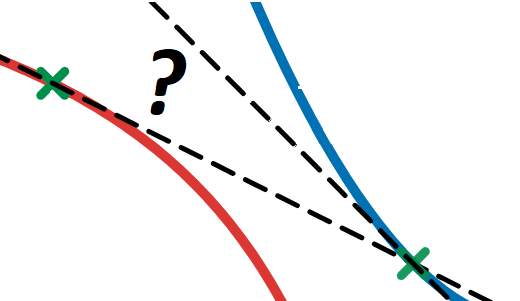
We aim to calculate the angle formed by the two dotted lines illustrated in Figure 1.

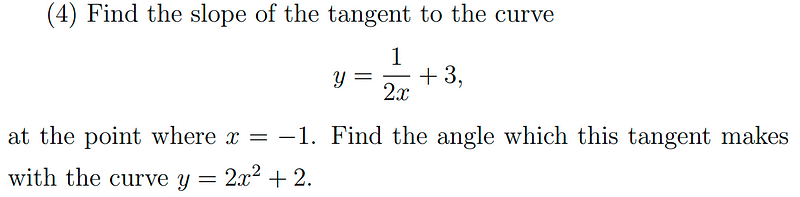
To find the slope of a tangent line at any given point, the first step is to compute the derivative of the function.

Next, evaluate the derivative at the specific point of interest.

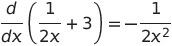
Once we have the slope, we need to determine the y-coordinate of the tangent point.

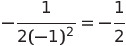
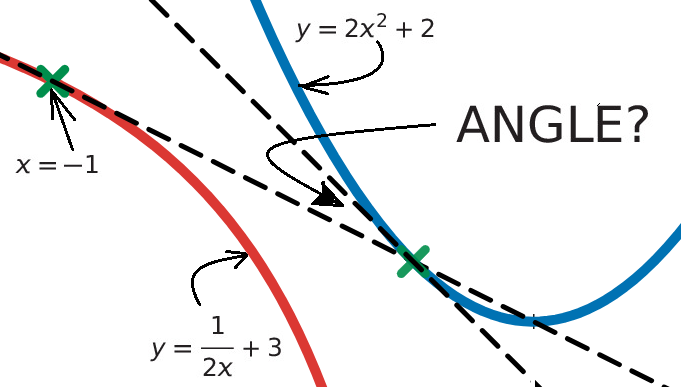
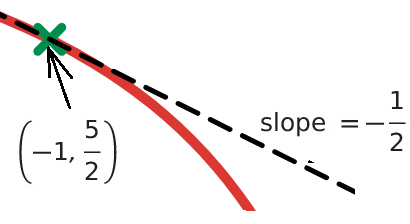
Let’s update Figure 1 with the newly acquired information.

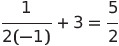
Now, with the slope and a point identified, we can write the tangent line in point-slope form and subsequently in slope-intercept form.

To find where the tangent line intersects the curve, equate the equations of the line and the curve.

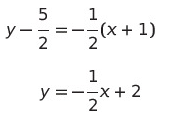
Substituting the solutions from this quadratic into either of the original equations yields the two points of intersection (refer to Figure 3).

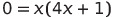
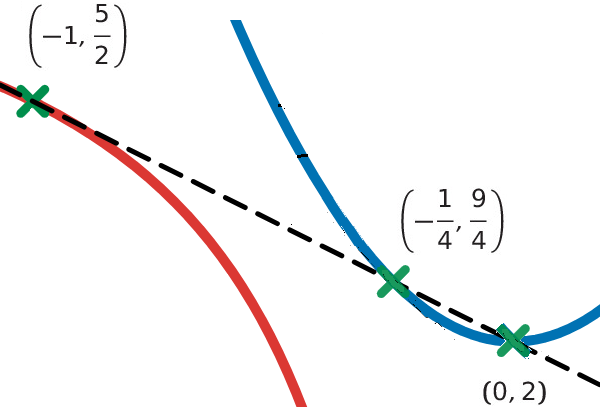
Next, we need the slopes of the curve at these intersection points. This requires taking the derivative of the function and evaluating it at each point.

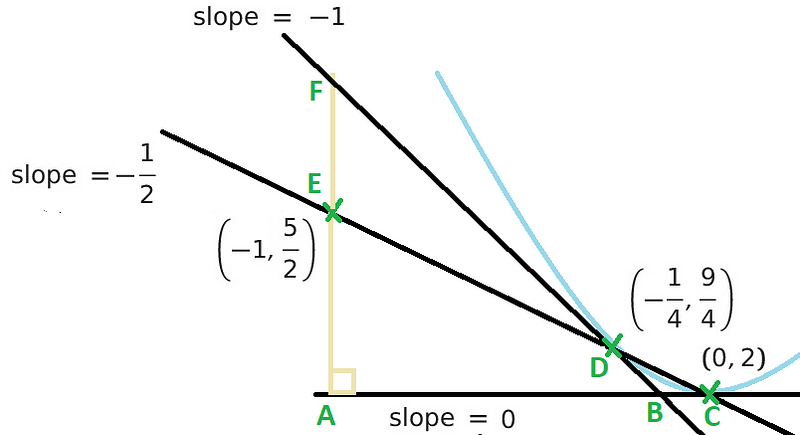
With three straight lines and their respective slopes determined, we can now convert this information into angles between the lines.

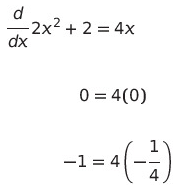
In Figure 4, angle ABF measures exactly 45 degrees. For angle ACE, we apply the inverse tangent function to find its value as ½. The angle we are ultimately interested in is angle EDF, which is the difference between these two angles.

Here’s the precise solution:

Although we could conclude here, let’s also approximate the angle in degrees.

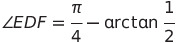
Bob’s your uncle!

The first video, "A Nifty Little Calculus Problem," dives into this fascinating topic, exploring various techniques and strategies for solving similar problems in calculus.

The second video, "Solving the Mathematics Calculus Problem in 'Gifted'," showcases how calculus concepts are applied in unique and engaging ways in popular media.